Ecuația tangentei la graficul funcției

P. Romanov, T. Romanova,
Magnitogorsk,
Regiunea Chelyabinsk

Ecuația tangentei la graficul funcției

Articolul a fost publicat cu sprijinul Complexului Hotelier ITAKA+. Stând în orașul constructorilor de nave Severodvinsk, nu vă veți confrunta cu problema găsirii de locuințe temporare. , pe site-ul complexului hotelier „ITAKA +” http://itakaplus.ru, puteți închiria ușor și rapid un apartament în oraș, pentru orice perioadă, cu plata zilnică.

În stadiul actual de dezvoltare a educației, una dintre sarcinile sale principale este formarea unei personalități care gândesc creativ. Capacitatea de creativitate la studenți poate fi dezvoltată numai dacă aceștia sunt implicați sistematic în bazele activităților de cercetare. Fundația pentru ca elevii să-și folosească forțele creative, abilitățile și talentele este formată de cunoștințe și abilități cu drepturi depline. În acest sens, problema formării unui sistem de cunoștințe și abilități de bază pentru fiecare subiect al cursului de matematică școlară este de o importanță nu mică. În același timp, abilitățile cu drepturi depline ar trebui să fie scopul didactic nu al sarcinilor individuale, ci al sistemului lor atent gândit. În sensul cel mai larg, un sistem este înțeles ca un set de elemente interconectate care interacționează care au integritate și o structură stabilă.

Luați în considerare o metodologie pentru a-i învăța pe elevi cum să întocmească o ecuație a unei tangente la un grafic de funcție. În esență, toate sarcinile pentru găsirea ecuației tangentei sunt reduse la necesitatea de a selecta din mulțimea (snop, familie) de linii pe acelea dintre ele care satisfac o anumită cerință - sunt tangente la graficul unei anumite funcții. În acest caz, setul de linii din care se efectuează selecția poate fi specificat în două moduri:

a) un punct situat pe planul xOy (creion central de linii);
b) coeficient unghiular (mănunchi paralel de linii).

În acest sens, la studierea subiectului „Tangentă la graficul unei funcții” pentru a izola elementele sistemului, am identificat două tipuri de sarcini:

1) sarcini pe o tangentă dată de un punct prin care trece;
2) sarcini pe o tangentă dată de panta acesteia.

Învățarea rezolvării problemelor pe o tangentă s-a realizat folosind algoritmul propus de A.G. Mordkovici. A lui diferenta fundamentala din cele deja cunoscute constă în faptul că abscisa punctului tangentei se notează cu litera a (în loc de x0), în legătură cu care ecuația tangentei ia forma

y \u003d f (a) + f "(a) (x - a)

(comparați cu y \u003d f (x 0) + f "(x 0) (x - x 0)). Această tehnică metodologică, în opinia noastră, permite elevilor să realizeze rapid și ușor unde sunt scrise coordonatele punctului curent în ecuația tangentei generale și unde sunt punctele de contact.

Algoritm pentru compilarea ecuației tangentei la graficul funcției y = f(x)

1. Desemnați cu litera a abscisa punctului de contact.
2. Găsiți f(a).
3. Găsiți f „(x) și f „(a).
4. Înlocuiți numerele găsite a, f (a), f "(a) în ecuația generală a tangentei y \u003d f (a) \u003d f "(a) (x - a).

Acest algoritm poate fi compilat pe baza selecției independente a operațiilor de către elevi și a secvenței de execuție a acestora.

Practica a arătat că soluția consecventă a fiecăreia dintre sarcinile cheie folosind algoritmul vă permite să vă formați capacitatea de a scrie ecuația tangentei la graficul funcției în etape, iar pașii algoritmului servesc drept puncte forte pentru acțiuni. . Această abordare corespunde teoriei formării treptate a acțiunilor mentale dezvoltată de P.Ya. Galperin și N.F. Talizina.

În primul tip de sarcini au fost identificate două sarcini cheie:

• tangenta trece printr-un punct situat pe curbă (problema 1);
• tangenta trece printr-un punct care nu se află pe curbă (Problema 2).

Sarcina 1. Echivalează tangenta cu graficul funcției în punctul M(3; – 2).

Soluţie. Punctul M(3; – 2) este punctul de contact, deoarece

1. a = 3 - abscisa punctului de atingere.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 este ecuația tangentei.

Sarcina 2. Scrieți ecuațiile tuturor tangentelor la graficul funcției y = - x 2 - 4x + 2, trecând prin punctul M(- 3; 6).

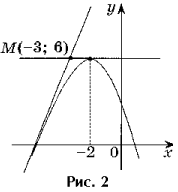Soluţie. Punctul M(– 3; 6) nu este un punct tangent, deoarece f(– 3) 6 (Fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - ecuație tangentă.

Tangenta trece prin punctul M(– 3; 6), prin urmare, coordonatele ei satisfac ecuația tangentei.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = - 4, a 2 = - 2.

Dacă a = – 4, atunci ecuația tangentei este y = 4x + 18.

Dacă a \u003d - 2, atunci ecuația tangentei are forma y \u003d 6.

În al doilea tip, sarcinile cheie vor fi următoarele:

• tangenta este paralelă cu o dreaptă (problema 3);
• tangenta trece la un anumit unghi la dreapta dată (Problema 4).

Sarcina 3. Scrieți ecuațiile tuturor tangentelor la graficul funcției y \u003d x 3 - 3x 2 + 3, paralele cu dreapta y \u003d 9x + 1.

Soluţie.

1. a - abscisa punctului de atingere.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Dar, pe de altă parte, f "(a) \u003d 9 (condiția de paralelism). Deci, trebuie să rezolvăm ecuația 3a 2 - 6a \u003d 9. Rădăcinile sale a \u003d - 1, a \u003d 3 (Fig. . 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 este ecuația tangentei;

1) a = 3;
2) f(3) = 3;
3) f „(3) = 9;
4) y = 3 + 9(x - 3);

y = 9x – 24 este ecuația tangentei.

Sarcina 4. Scrieți ecuația tangentei la graficul funcției y = 0,5x 2 - 3x + 1, trecând cu un unghi de 45 ° la dreapta y = 0 (Fig. 4).

Soluţie. Din condiția f "(a) \u003d tg 45 ° găsim a: a - 3 \u003d 1^a=4.

1. a = 4 - abscisa punctului de atingere.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - ecuația tangentei.

Este ușor de demonstrat că rezolvarea oricărei alte probleme se reduce la rezolvarea uneia sau mai multor probleme cheie. Luați în considerare următoarele două probleme ca exemplu.

1. Scrieți ecuațiile tangentelor la parabola y = 2x 2 - 5x - 2, dacă tangentele se intersectează în unghi drept și una dintre ele atinge parabola în punctul cu abscisa 3 (Fig. 5).

Soluţie. Deoarece abscisa punctului de contact este dată, prima parte a soluției se reduce la problema cheie 1.

1. a \u003d 3 - abscisa punctului de contact al uneia dintre laturile unghiului drept.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - ecuația primei tangente.

Lasă a este unghiul de înclinare al primei tangente. Deoarece tangentele sunt perpendiculare, atunci este unghiul de înclinare al celei de-a doua tangente. Din ecuația y = 7x – 20 a primei tangente avem tg a = 7. Găsiți

Aceasta înseamnă că panta celei de-a doua tangente este .

Soluția ulterioară se reduce la sarcina cheie 3.

Fie B(c; f(c)) punctul tangent al celei de-a doua drepte, atunci

1. - abscisa celui de-al doilea punct de contact.
2.
3.
4.
este ecuația celei de-a doua tangente.

Notă. Coeficientul unghiular al tangentei poate fi găsit mai ușor dacă elevii cunosc raportul dintre coeficienții dreptelor perpendiculare k 1 k 2 = - 1.

2. Scrieți ecuațiile tuturor tangentelor comune la graficele de funcții

Soluţie. Sarcina se reduce la găsirea absciselor punctelor de contact ale tangentelor comune, adică la rezolvarea problemei cheie 1 într-o formă generală, alcătuirea unui sistem de ecuații și apoi rezolvarea acestuia (Fig. 6).

1. Fie a abscisa punctului de atingere situat pe graficul funcției y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f „(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.

1. Fie c abscisa punctului tangent situat pe graficul funcției
2.
3. f „(c) = c.
4.

Din moment ce tangentele sunt comune, atunci

Deci y = x + 1 și y = - 3x - 3 sunt tangente comune.

Scopul principal al sarcinilor luate în considerare este pregătirea elevilor pentru auto-recunoașterea tipului de sarcină cheie atunci când rezolvă sarcini mai complexe care necesită anumite abilități de cercetare (capacitatea de a analiza, compara, generaliza, formula o ipoteză etc.). Astfel de sarcini includ orice sarcină în care sarcina cheie este inclusă ca componentă. Să luăm ca exemplu problema (invers cu problema 1) de a găsi o funcție din familia tangentelor sale.

3. Pentru ce b și c sunt liniile y \u003d x și y \u003d - 2x tangente la graficul funcției y \u003d x 2 + bx + c?

Soluţie.

Fie t abscisa punctului de contact al dreptei y = x cu parabola y = x 2 + bx + c; p este abscisa punctului de contact al dreptei y = - 2x cu parabola y = x 2 + bx + c. Atunci ecuația tangentei y = x va lua forma y = (2t + b)x + c - t 2 , iar ecuația tangentei y = - 2x va lua forma y = (2p + b)x + c - p 2 .

Compuneți și rezolvați un sistem de ecuații

Răspuns:

Sarcini pentru soluție independentă

1. Scrieți ecuațiile tangentelor trasate la graficul funcției y = 2x 2 - 4x + 3 în punctele de intersecție ale graficului cu dreapta y = x + 3.

Răspuns: y \u003d - 4x + 3, y \u003d 6x - 9,5.

2. Pentru ce valori ale lui a trece tangenta desenată la graficul funcției y \u003d x 2 - ax în punctul graficului cu abscisa x 0 \u003d 1 prin punctul M (2; 3) ?

Răspuns: a = 0,5.

3. Pentru ce valori ale lui p linia y = px - 5 atinge curba y = 3x 2 - 4x - 2?

Răspuns: p 1 \u003d - 10, p 2 \u003d 2.

4. Aflați toate punctele comune ale graficului funcției y = 3x - x 3 și tangenta trasată la acest grafic prin punctul P(0; 16).

Răspuns: A(2; - 2), B(- 4; 52).

5. Aflați cea mai scurtă distanță dintre parabolă y = x 2 + 6x + 10 și linie

Răspuns:

6. Pe curba y \u003d x 2 - x + 1, găsiți punctul în care tangenta la grafic este paralelă cu linia y - 3x + 1 \u003d 0.

Răspuns: M(2; 3).

7. Scrieți ecuația tangentei la graficul funcției y = x 2 + 2x - | 4x | care îl atinge în două puncte. Faceți un desen.

Răspuns: y = 2x - 4.

8. Demonstrați că dreapta y = 2x – 1 nu intersectează curba y = x 4 + 3x 2 + 2x. Găsiți distanța dintre cele mai apropiate puncte ale acestora.

Răspuns:

9. Pe parabola y \u003d x 2, sunt luate două puncte cu abscise x 1 \u003d 1, x 2 \u003d 3. Prin aceste puncte se trasează o secantă. În ce punct al parabolei tangenta la aceasta va fi paralelă cu secantei desenate? Scrieți ecuațiile secantei și tangentei.

Răspuns: y \u003d 4x - 3 - ecuație secante; y = 4x – 4 este ecuația tangentei.

10. Aflați unghiul q între tangentele la graficul funcției y \u003d x 3 - 4x 2 + 3x + 1, desenate în puncte cu abscisele 0 și 1.

Răspuns: q = 45°.

11. În ce puncte tangenta la graficul funcției formează un unghi de 135° cu axa Ox?

Răspuns: A(0; - 1), B(4; 3).

12. În punctul A(1; 8) la curbă se trasează o tangentă. Aflați lungimea segmentului tangentei cuprins între axele de coordonate.

Răspuns:

13. Scrieți ecuația tuturor tangentelor comune la graficele funcțiilor y \u003d x 2 - x + 1 și y \u003d 2x 2 - x + 0,5.

Răspuns: y = - 3x și y = x.

14. Aflați distanța dintre tangente la graficul funcției paralel cu axa x.

Răspuns:

15. Determinați la ce unghiuri intersectează parabola y \u003d x 2 + 2x - 8 axa x.

Răspuns: q 1 \u003d arctan 6, q 2 \u003d arctan (- 6).

16. Pe graficul funcţiei găsiți toate punctele, tangenta la fiecare dintre ele la acest grafic intersectează semiaxele pozitive ale coordonatelor, decupând segmente egale din ele.

Răspuns: A(-3; 11).

17. Linia y = 2x + 7 și parabola y = x 2 – 1 se intersectează în punctele M și N. Aflați punctul de intersecție K al dreptelor tangente la parabolă în punctele M și N.

Răspuns: K(1; - 9).

18. Pentru ce valori ale lui b este linia y \u003d 9x + b tangentă la graficul funcției y \u003d x 3 - 3x + 15?

Raspunsul 1; 31.

19. Pentru ce valori ale lui k linia y = kx – 10 are un singur punct comun cu graficul funcției y = 2x 2 + 3x – 2? Pentru valorile găsite ale lui k, determinați coordonatele punctului.

Răspuns: k 1 = - 5, A(- 2; 0); k2 = 11, B(2; 12).

20. Pentru ce valori ale lui b trece tangenta trasată la graficul funcției y = bx 3 – 2x 2 – 4 în punctul cu abscisa x 0 = 2 prin punctul M(1; 8)?

Răspuns: b = - 3.

21. O parabolă cu un vârf pe axa x este tangentă la o dreaptă care trece prin punctele A(1; 2) și B(2; 4) în punctul B. Aflați ecuația parabolei.

Răspuns:

22. La ce valoare a coeficientului k atinge parabola y \u003d x 2 + kx + 1 de axa Ox?

Răspuns: k = q 2.

23. Aflați unghiurile dintre dreapta y = x + 2 și curba y = 2x 2 + 4x - 3.

29. Aflați distanța dintre tangentele la graficul generatoarelor de funcții cu direcția pozitivă a axei Ox la un unghi de 45 °.

Răspuns:

30. Aflați locul vârfurilor tuturor parabolelor de forma y = x 2 + ax + b atingând dreapta y = 4x - 1.

Răspuns: linie dreaptă y = 4x + 3.

Literatură

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra și începuturile analizei: 3600 de probleme pentru școlari și solicitanții la universitate. - M., Butarda, 1999.
2. Mordkovich A. Al patrulea seminar pentru tineri profesori. Subiectul este „Aplicații derivate”. - M., „Matematică”, Nr. 21/94.
3. Formarea de cunoștințe și deprinderi pe baza teoriei asimilării treptate a acțiunilor mentale. / Ed. P.Ya. Galperin, N.F. Talizina. - M., Universitatea de Stat din Moscova, 1968.

Luați în considerare următoarea figură:

Arată o funcție y = f(x) care este diferențiabilă în punctul a. Punctul marcat M cu coordonatele (a; f(a)). Printr-un punct arbitrar P(a + ∆x; f(a + ∆x)) al graficului, se trasează o secanta MP.

Dacă acum punctul P este deplasat de-a lungul graficului către punctul M, atunci linia dreaptă MP se va roti în jurul punctului M. În acest caz, ∆x va tinde spre zero. De aici putem formula definiția unei tangente la graficul unei funcții.

Graficul tangent la funcție

Tangenta la graficul funcției este poziția limită a secantei atunci când incrementul argumentului tinde spre zero. Trebuie înțeles că existența derivatei funcției f în punctul x0 înseamnă că în acest punct al graficului există tangentă către el.

În acest caz, panta tangentei va fi egală cu derivata acestei funcții în acest punct f’(x0). Acesta este sensul geometric al derivatului. Tangenta la graficul functiei f diferentiabila in punctul x0 este o dreapta care trece prin punctul (x0;f(x0)) si avand o panta f’(x0).

Ecuația tangentei

Să încercăm să obținem ecuația tangentei la graficul unei funcții f în punctul A(x0; f(x0)). Ecuația unei drepte cu panta k are următoarea formă:

Deoarece panta noastră este egală cu derivata f'(x0), atunci ecuația va lua următoarea formă: y = f'(x0)*x + b.

Acum să calculăm valoarea lui b. Pentru a face acest lucru, folosim faptul că funcția trece prin punctul A.

f(x0) = f’(x0)*x0 + b, de aici exprimăm b și obținem b = f(x0) - f’(x0)*x0.

Inlocuim valoarea rezultata in ecuatia tangentei:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Luați în considerare următorul exemplu: găsiți ecuația tangentei la graficul funcției f (x) \u003d x 3 - 2 * x 2 + 1 în punctul x \u003d 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Înlocuiți valorile obținute în formula tangentei, obținem: y = 1 + 4*(x - 2). Deschizând parantezele și aducând termeni similari, obținem: y = 4*x - 7.

Răspuns: y = 4*x - 7.

Schema generala de compilare a ecuatiei tangentei la graficul funcției y = f(x):

1. Determinați x0.

2. Calculați f(x0).

3. Calculați f'(x)

Instruire

Determinăm panta tangentei la curbă în punctul M.
Curba care reprezintă graficul funcției y = f(x) este continuă într-o apropiere a punctului M (inclusiv punctul M însuși).

Dacă valoarea f‘(x0) nu există, atunci fie nu există tangentă, fie trece vertical. Având în vedere acest lucru, prezența derivatei funcției în punctul x0 se datorează existenței unei tangente neverticale care se află în contact cu graficul funcției în punctul (x0, f(x0)). În acest caz, panta tangentei va fi egală cu f "(x0). Astfel, sensul geometric al derivatei devine clar - calculul pantei tangentei.

Aflați valoarea abscisei punctului de contact, care este notat cu litera „a”. Dacă coincide cu punctul tangent dat, atunci „a” va fi coordonata sa x. Determinați valoarea funcții f(a), înlocuind în ecuație funcții dimensiunea abscisei.

Determinați prima derivată a ecuației funcții f'(x) și înlocuiți valoarea punctului „a”.

Luați ecuația tangentă generală, care este definită ca y \u003d f (a) \u003d f (a) (x - a) și înlocuiți valorile găsite pentru a, f (a), f "( a) în ea. Ca urmare, se va găsi soluția graficului și se va găsi tangentă.

Rezolvați problema într-un mod diferit dacă punctul tangent dat nu a coincis cu punctul tangent. În acest caz, este necesar să înlocuiți „a” în loc de numere în ecuația tangentei. După aceea, în loc de literele „x” și „y”, înlocuiți valoarea coordonatelor punct dat. Rezolvați ecuația rezultată în care „a” este necunoscutul. Puneți valoarea rezultată în ecuația tangentei.

Scrieți o ecuație pentru o tangentă cu litera „a”, dacă ecuația este dată în condiția problemei funcțiiși ecuația unei drepte paralele în raport cu tangentei dorite. După aceea, aveți nevoie de un derivat funcții la coordonata din punctul „a”. Introduceți valoarea corespunzătoare în ecuația tangentei și rezolvați funcția.

Exemplul 1 Dată o funcție f(X) = 3X 2 + 4X– 5. Să scriem ecuația tangentei la graficul funcției f(X) în punctul graficului cu abscisa X 0 = 1.

Soluţie. Derivată de funcție f(X) există pentru orice x R . Să-l găsim:

= (3X 2 + 4X– 5)′ = 6 X + 4.

Apoi f(X 0) = f(1) = 2; (X 0) = = 10. Ecuația tangentei are forma:

y = (X 0) (X – X 0) + f(X 0),

y = 10(X – 1) + 2,

y = 10X – 8.

Răspuns. y = 10X – 8.

Exemplul 2 Dată o funcție f(X) = X 3 – 3X 2 + 2X+ 5. Să scriem ecuația tangentei la graficul funcției f(X), paralel cu linia y = 2X – 11.

Soluţie. Derivată de funcție f(X) există pentru orice x R . Să-l găsim:

= (X 3 – 3X 2 + 2X+ 5)′ = 3 X 2 – 6X + 2.

Deoarece tangenta la graficul functiei f(X) în punctul cu abscisa X 0 este paralel cu dreapta y = 2X– 11, atunci panta sa este 2, adică ( X 0) = 2. Găsiți această abscisă din condiția ca 3 X– 6X 0 + 2 = 2. Această egalitate este valabilă numai pentru X 0 = 0 și X 0 = 2. Întrucât în ​​ambele cazuri f(X 0) = 5, apoi linia dreaptă y = 2X + b atinge graficul funcției fie în punctul (0; 5), fie în punctul (2; 5).

În primul caz, egalitatea numerică este adevărată 5 = 2×0 + b, Unde b= 5, iar în al doilea caz, egalitatea numerică este adevărată 5 = 2 × 2 + b, Unde b = 1.

Deci sunt două tangente y = 2X+ 5 și y = 2X+ 1 la graficul funcției f(X) paralel cu dreapta y = 2X – 11.

Răspuns. y = 2X + 5, y = 2X + 1.

Exemplul 3 Dată o funcție f(X) = X 2 – 6X+ 7. Să scriem ecuația tangentei la graficul funcției f(X) trecând prin punct A (2; –5).

Soluţie. pentru că f(2) –5, apoi punctul A nu aparține graficului funcției f(X). Lăsa X 0 - abscisa punctului de atingere.

Derivată de funcție f(X) există pentru orice x R . Să-l găsim:

= (X 2 – 6X+ 1)′ = 2 X – 6.

Apoi f(X 0) = X– 6X 0 + 7; (X 0) = 2X 0 - 6. Ecuația tangentei are forma:

y = (2X 0 – 6)(X – X 0) + X– 6X+ 7,

y = (2X 0 – 6)X– X+ 7.

De la punctul A aparține tangentei, atunci egalitatea numerică este adevărată

–5 = (2X 0 – 6)×2– X+ 7,

Unde X 0 = 0 sau X 0 = 4. Aceasta înseamnă că prin punct A este posibil să se deseneze două tangente la graficul funcției f(X).

În cazul în care un X 0 = 0, atunci ecuația tangentei are forma y = –6X+ 7. Dacă X 0 = 4, atunci ecuația tangentei are forma y = 2X – 9.

Răspuns. y = –6X + 7, y = 2X – 9.

Exemplul 4 Funcții date f(X) = X 2 – 2X+ 2 și g(X) = –X 2 - 3. Să scriem ecuația tangentei comune la graficele acestor funcții.

Soluţie. Lăsa X 1 - abscisa punctului de contact al dreptei dorite cu graficul functiei f(X), A X 2 - abscisa punctului de contact al aceleiasi drepte cu graficul functiei g(X).

Derivată de funcție f(X) există pentru orice x R . Să-l găsim:

= (X 2 – 2X+ 2)′ = 2 X – 2.

Apoi f(X 1) = X– 2X 1 + 2; (X 1) = 2X 1 - 2. Ecuația tangentei are forma:

y = (2X 1 – 2)(X – X 1) + X– 2X 1 + 2,

y = (2X 1 – 2)X – X+ 2. (1)

Să găsim derivata funcției g(X):

= (–X 2 – 3)′ = –2 X.

Să fie dată o funcție f, care la un punct x 0 are o derivată finită f (x 0). Apoi, dreapta care trece prin punctul (x 0; f (x 0)), care are o pantă f '(x 0), se numește tangentă.

Dar ce se întâmplă dacă derivata în punctul x 0 nu există? Există două opțiuni:

1. Nici tangenta la grafic nu există. Exemplul clasic este funcția y = |x | în punctul (0; 0).
2. Tangenta devine verticală. Acest lucru este adevărat, de exemplu, pentru funcția y = arcsin x în punctul (1; π /2).

Ecuația tangentei

Orice dreaptă neverticală este dată de o ecuație de forma y = kx + b, unde k este panta. Tangenta nu face excepție, iar pentru a-și compune ecuația la un punct x 0 este suficient să cunoaștem valoarea funcției și a derivatei în acest punct.

Deci, să fie dată o funcție y \u003d f (x), care are o derivată y \u003d f '(x) pe segment. Atunci în orice punct x 0 ∈ (a; b) se poate trasa o tangentă la graficul acestei funcții, care este dată de ecuația:

y \u003d f '(x 0) (x - x 0) + f (x 0)

Aici f ’(x 0) este valoarea derivatei în punctul x 0, iar f (x 0) este valoarea funcției în sine.

O sarcină. Având în vedere o funcție y = x 3 . Scrieți o ecuație pentru tangenta la graficul acestei funcții în punctul x 0 = 2.

Ecuație tangentă: y \u003d f '(x 0) (x - x 0) + f (x 0). Punctul x 0 = 2 ne este dat, dar valorile f (x 0) și f '(x 0) vor trebui calculate.

Mai întâi, să găsim valoarea funcției. Totul este ușor aici: f (x 0) = f (2) = 2 3 = 8;
Acum să găsim derivata: f '(x) \u003d (x 3) ' \u003d 3x 2;
Înlocuiți în derivată x 0 = 2: f '(x 0) = f '(2) = 3 2 2 = 12;
Deci obținem: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
Aceasta este ecuația tangentei.

O sarcină. Compuneți ecuația tangentei la graficul funcției f (x) \u003d 2sin x + 5 în punctul x 0 \u003d π / 2.

De data aceasta nu vom descrie în detaliu fiecare acțiune - vom indica doar pașii cheie. Avem:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

Ecuația tangentei:

y = 0 (x − π /2) + 7 ⇒ y = 7

În acest din urmă caz, linia s-a dovedit a fi orizontală, deoarece panta sa k = 0. Nu este nimic în neregulă cu asta - tocmai am dat peste un punct extremum.