L'équation de la tangente au graphe de la fonction

P. Romanov, T. Romanova,
Magnitogorsk,
Région de Tcheliabinsk

L'équation de la tangente au graphe de la fonction

L'article a été publié avec le soutien du complexe hôtelier ITAKA+. En séjournant dans la ville des constructeurs navals de Severodvinsk, vous ne rencontrerez pas le problème de trouver un logement temporaire. , sur le site Web du complexe hôtelier "ITAKA +" http://itakaplus.ru, vous pouvez facilement et rapidement louer un appartement dans la ville, pour n'importe quelle période, avec un paiement journalier.

Au stade actuel de développement de l'éducation, l'une de ses tâches principales est la formation d'une personnalité pensant de manière créative. La capacité de créativité des étudiants ne peut être développée que s'ils sont systématiquement impliqués dans les bases des activités de recherche. La base pour que les étudiants utilisent leurs forces créatives, leurs capacités et leurs talents est formée de connaissances et de compétences à part entière. À cet égard, le problème de la formation d'un système de connaissances et de compétences de base pour chaque sujet du cours de mathématiques à l'école n'est pas sans importance. Dans le même temps, les compétences à part entière devraient être l'objectif didactique non pas des tâches individuelles, mais de leur système soigneusement pensé. Au sens le plus large, un système est compris comme un ensemble d'éléments interdépendants qui ont une intégrité et une structure stable.

Envisagez une méthodologie pour enseigner aux élèves comment établir une équation d'une tangente à un graphique de fonction. Essentiellement, toutes les tâches de recherche de l'équation tangente sont réduites à la nécessité de sélectionner dans l'ensemble (faisceau, famille) de lignes celles qui satisfont à une certaine exigence - elles sont tangentes au graphique d'une certaine fonction. Dans ce cas, l'ensemble des lignes à partir desquelles la sélection est effectuée peut être spécifié de deux manières :

a) un point situé sur le plan xOy (crayon central de droites) ;
b) coefficient angulaire (faisceau de lignes parallèles).

A cet égard, lors de l'étude du sujet "Tangente au graphe d'une fonction" afin d'isoler les éléments du système, nous avons identifié deux types de tâches :

1) tâches sur une tangente donnée par un point par lequel elle passe ;
2) tâches sur une tangente donnée par sa pente.

L'apprentissage de la résolution de problèmes sur une tangente a été réalisé à l'aide de l'algorithme proposé par A.G. Mordkovitch. Le sien différence fondamentale du déjà connu réside dans le fait que l'abscisse du point tangent est désignée par la lettre a (au lieu de x0), en relation avec laquelle l'équation de la tangente prend la forme

y \u003d f (a) + f "(a) (x - a)

(comparer avec y \u003d f (x 0) + f "(x 0) (x - x 0)). Cette technique méthodologique, à notre avis, permet aux étudiants de se rendre compte rapidement et facilement où les coordonnées du point actuel sont écrites dans l'équation générale de la tangente, et où sont les points de contact.

Algorithme pour compiler l'équation de la tangente au graphe de la fonction y = f(x)

1. Désigner par la lettre a l'abscisse du point de contact.
2. Trouver f(a).
3. Trouvez f "(x) et f "(a).
4. Remplacez les nombres trouvés a, f (a), f "(a) dans l'équation générale de la tangente y \u003d f (a) \u003d f "(a) (x - a).

Cet algorithme peut être compilé sur la base de la sélection indépendante des opérations par les élèves et de la séquence de leur exécution.

La pratique a montré que la solution cohérente de chacune des tâches clés à l'aide de l'algorithme vous permet de former la capacité d'écrire l'équation de la tangente au graphique de la fonction par étapes, et les étapes de l'algorithme servent de points forts pour les actions . Cette approche correspond à la théorie de la formation progressive des actions mentales développée par P.Ya. Galperin et N.F. Talyzina.

Dans le premier type de tâches, deux tâches clés ont été identifiées :

• la tangente passe par un point situé sur la courbe (problème 1) ;
• la tangente passe par un point non situé sur la courbe (problème 2).

Tâche 1. Équation de la tangente au graphique de la fonction au point M(3; – 2).

La solution. Le point M(3; – 2) est le point de contact, puisque

1. a = 3 - abscisse du point de contact.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 est l'équation tangente.

Tâche 2. Écrivez les équations de toutes les tangentes au graphique de la fonction y = - x 2 - 4x + 2, passant par le point M(- 3; 6).

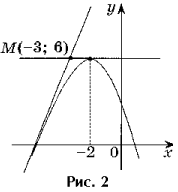La solution. Le point M(– 3; 6) n'est pas un point tangent, puisque f(– 3) 6 (fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - équation tangente.

La tangente passe par le point M(– 3; 6), par conséquent, ses coordonnées satisfont l'équation de la tangente.

6 = – une 2 – 4a + 2 – 2(une + 2)(– 3 – une),
un 2 + 6a + 8 = 0^ un 1 = - 4, un 2 = - 2.

Si a = – 4, alors l'équation tangente est y = 4x + 18.

Si a \u003d - 2, alors l'équation tangente a la forme y \u003d 6.

Dans le second type, les tâches clés seront les suivantes :

• la tangente est parallèle à une droite (problème 3) ;
• la tangente passe à un certain angle par rapport à la ligne donnée (problème 4).

Tâche 3. Écrivez les équations de toutes les tangentes au graphique de la fonction y \u003d x 3 - 3x 2 + 3, parallèle à la ligne y \u003d 9x + 1.

La solution.

1. a - abscisse du point de contact.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Mais, d'autre part, f "(a) \u003d 9 (condition de parallélisme). Nous devons donc résoudre l'équation 3a 2 - 6a \u003d 9. Ses racines a \u003d - 1, a \u003d 3 (Fig 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9 ;
4) y = – 1 + 9(x + 1);

y = 9x + 8 est l'équation tangente ;

1) un = 3 ;
2) f(3) = 3 ;
3) f "(3) = 9 ;
4) y = 3 + 9(x - 3);

y = 9x – 24 est l'équation tangente.

Tâche 4. Écrivez l'équation de la tangente au graphique de la fonction y = 0,5x 2 - 3x + 1, en passant sous un angle de 45 ° par rapport à la droite y = 0 (Fig. 4).

La solution. A partir de la condition f "(a) \u003d tg 45 ° on trouve a: a - 3 \u003d 1^a=4.

1. a = 4 - abscisse du point de contact.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - l'équation de la tangente.

Il est facile de montrer que la solution de tout autre problème se réduit à la solution d'un ou plusieurs problèmes clés. Considérons les deux problèmes suivants à titre d'exemple.

1. Écrivez les équations des tangentes à la parabole y = 2x 2 - 5x - 2, si les tangentes se coupent à angle droit et que l'une d'elles touche la parabole au point d'abscisse 3 (Fig. 5).

La solution. L'abscisse du point de contact étant donnée, la première partie de la solution se réduit au problème clé 1.

1. a \u003d 3 - l'abscisse du point de contact de l'un des côtés de l'angle droit.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - l'équation de la première tangente.

Laissez un est l'angle d'inclinaison de la première tangente. Puisque les tangentes sont perpendiculaires, alors est l'angle d'inclinaison de la deuxième tangente. De l'équation y = 7x – 20 de la première tangente nous avons tg a = 7. Trouver

Cela signifie que la pente de la deuxième tangente est .

La solution supplémentaire est réduite à la tâche clé 3.

Soit B(c; f(c)) le point tangent de la seconde droite, alors

1. - abscisse du deuxième point de contact.
2.
3.
4.
est l'équation de la deuxième tangente.

Noter. Le coefficient angulaire de la tangente peut être trouvé plus facilement si les élèves connaissent le rapport des coefficients des droites perpendiculaires k 1 k 2 = - 1.

2. Écrivez les équations de toutes les tangentes communes aux graphiques de fonctions

La solution. La tâche est réduite à trouver les abscisses des points de contact des tangentes communes, c'est-à-dire à résoudre le problème clé 1 sous une forme générale, à compiler un système d'équations puis à le résoudre (Fig. 6).

1. Soit a l'abscisse du point de contact situé sur le graphique de la fonction y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y \u003d une 2 + une + 1 + (2a + 1) (x - une) \u003d (2a + 1) x + 1 - une 2.

1. Soit c l'abscisse du point tangent situé sur le graphe de la fonction
2.
3. f "(c) = c.
4.

Les tangentes étant communes, alors

Donc y = x + 1 et y = - 3x - 3 sont des tangentes communes.

L'objectif principal des tâches envisagées est de préparer les élèves à l'auto-reconnaissance du type de tâche clé lors de la résolution de tâches plus complexes nécessitant certaines compétences de recherche (capacité d'analyse, de comparaison, de généralisation, d'hypothèse, etc.). Ces tâches incluent toute tâche dans laquelle la tâche clé est incluse en tant que composant. Considérons à titre d'exemple le problème (inverse du problème 1) de trouver une fonction à partir de la famille de ses tangentes.

3. Pour quoi b et c sont les lignes y \u003d x et y \u003d - 2x tangentes au graphique de la fonction y \u003d x 2 + bx + c ?

La solution.

Soit t l'abscisse du point de contact de la droite y = x avec la parabole y = x 2 + bx + c ; p est l'abscisse du point de contact de la droite y = - 2x avec la parabole y = x 2 + bx + c. Alors l'équation tangente y = x prendra la forme y = (2t + b)x + c - t 2 , et l'équation tangente y = - 2x prendra la forme y = (2p + b)x + c - p 2 .

Composer et résoudre un système d'équations

Réponse:

Tâches pour une solution indépendante

1. Écrivez les équations des tangentes tracées au graphique de la fonction y = 2x 2 - 4x + 3 aux points d'intersection du graphique avec la ligne y = x + 3.

Réponse : y \u003d - 4x + 3, y \u003d 6x - 9,5.

2. Pour quelles valeurs de a la tangente tracée au graphique de la fonction y \u003d x 2 - ax au point du graphique avec l'abscisse x 0 \u003d 1 passe-t-elle par le point M (2; 3) ?

Réponse : a = 0,5.

3. Pour quelles valeurs de p la ligne y = px - 5 touche-t-elle la courbe y = 3x 2 - 4x - 2 ?

Réponse : p 1 \u003d - 10, p 2 \u003d 2.

4. Trouver tous les points communs du graphe de la fonction y = 3x - x 3 et la tangente tracée à ce graphe passant par le point P(0; 16).

Réponse : A(2 ; - 2), B(- 4 ; 52).

5. Trouvez la distance la plus courte entre la parabole y = x 2 + 6x + 10 et la droite

Réponse:

6. Sur la courbe y \u003d x 2 - x + 1, trouvez le point auquel la tangente au graphique est parallèle à la ligne y - 3x + 1 \u003d 0.

Réponse : M(2 ; 3).

7. Écrivez l'équation de la tangente au graphique de la fonction y = x 2 + 2x - | 4x | qui le touche en deux points. Faites un dessin.

Réponse : y = 2x - 4.

8. Démontrer que la droite y = 2x – 1 ne coupe pas la courbe y = x 4 + 3x 2 + 2x. Trouver la distance entre leurs points les plus proches.

Réponse:

9. Sur la parabole y \u003d x 2, on prend deux points avec les abscisses x 1 \u003d 1, x 2 \u003d 3. Une sécante est tracée à travers ces points. En quel point de la parabole la tangente à celle-ci sera-t-elle parallèle à la sécante dessinée ? Écris les équations de la sécante et de la tangente.

Réponse: y \u003d 4x - 3 - équation sécante; y = 4x – 4 est l'équation tangente.

10. Trouvez l'angle q entre les tangentes au graphique de la fonction y \u003d x 3 - 4x 2 + 3x + 1, tracée aux points d'abscisse 0 et 1.

Réponse : q = 45°.

11. En quels points la tangente à la fonction graphique forme-t-elle un angle de 135° avec l'axe Ox ?

Réponse : A(0 ; - 1), B(4 ; 3).

12. Au point A(1; 8) de la courbe une tangente est tracée. Trouvez la longueur du segment tangent compris entre les axes de coordonnées.

Réponse:

13. Écrivez l'équation de toutes les tangentes communes aux graphiques des fonctions y \u003d x 2 - x + 1 et y \u003d 2x 2 - x + 0,5.

Réponse : y = - 3x et y = x.

14. Trouvez la distance entre les tangentes au graphique de la fonction parallèle à l'axe des x.

Réponse:

15. Déterminez à quels angles la parabole y \u003d x 2 + 2x - 8 coupe l'axe des x.

Réponse : q 1 \u003d arctan 6, q 2 \u003d arctan (- 6).

16. Sur le graphique de la fonction trouver tous les points dont la tangente à chacun de ce graphique coupe les demi-axes positifs de coordonnées, en coupant des segments égaux.

Réponse : A(-3 ; 11).

17. La droite y = 2x + 7 et la parabole y = x 2 – 1 se coupent aux points M et N. Trouvez le point d'intersection K des droites tangentes à la parabole aux points M et N.

Réponse : K(1 ; - 9).

18. Pour quelles valeurs de b la ligne y \u003d 9x + b est-elle tangente au graphique de la fonction y \u003d x 3 - 3x + 15 ?

Réponse 1; 31.

19. Pour quelles valeurs de k la droite y = kx – 10 n'a-t-elle qu'un seul point commun avec le graphique de la fonction y = 2x 2 + 3x – 2 ? Pour les valeurs trouvées de k, déterminez les coordonnées du point.

Réponse : k 1 = - 5, A(- 2 ; 0) ; k 2 = 11, B(2; 12).

20. Pour quelles valeurs de b la tangente tracée au graphique de la fonction y = bx 3 – 2x 2 – 4 au point d'abscisse x 0 = 2 passe-t-elle par le point M(1 ; 8) ?

Réponse : b = - 3.

21. Une parabole avec un sommet sur l'axe des x est tangente à une droite passant par les points A(1; 2) et B(2; 4) au point B. Trouvez l'équation de la parabole.

Réponse:

22. À quelle valeur du coefficient k la parabole y \u003d x 2 + kx + 1 touche-t-elle l'axe Ox ?

Réponse : k = q 2.

23. Trouvez les angles entre la ligne y = x + 2 et la courbe y = 2x 2 + 4x - 3.

29. Trouvez la distance entre les tangentes au graphique des générateurs de fonctions avec la direction positive de l'axe Ox à un angle de 45 °.

Réponse:

30. Trouvez le lieu des sommets de toutes les paraboles de la forme y = x 2 + ax + b touchant la ligne y = 4x - 1.

Réponse : droite y = 4x + 3.

Littérature

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algèbre et débuts de l'analyse : 3 600 problèmes pour les écoliers et les candidats à l'université. - M., Outarde, 1999.
2. Mordkovich A. Le quatrième séminaire pour les jeunes enseignants. Le sujet est "Applications dérivées". - M., "Mathématiques", n° 21/94.
3. Formation de connaissances et de compétences basées sur la théorie de l'assimilation progressive des actions mentales. / Éd. P.Ya. Galperin, N.F. Talyzina. - M., Université d'État de Moscou, 1968.

Considérez la figure suivante :

Il montre une fonction y = f(x) qui est différentiable au point a. Point marqué M avec les coordonnées (a; f(a)). Par un point arbitraire P(a + ∆x; f(a + ∆x)) du graphe, une sécante MP est tracée.

Si maintenant le point P est décalé le long du graphique vers le point M, alors la droite MP tournera autour du point M. Dans ce cas, ∆x tendra vers zéro. De là, nous pouvons formuler la définition d'une tangente au graphe d'une fonction.

Tangente au graphe de fonction

La tangente au graphe de la fonction est la position limite de la sécante lorsque l'incrément de l'argument tend vers zéro. Il faut comprendre que l'existence de la dérivée de la fonction f au point x0 signifie qu'en ce point du graphique il y a tangenteà lui.

Dans ce cas, la pente de la tangente sera égale à la dérivée de cette fonction en ce point f'(x0). C'est le sens géométrique de la dérivée. La tangente au graphe de la fonction f différentiable au point x0 est une droite quelconque passant par le point (x0;f(x0)) et ayant une pente f’(x0).

Équation tangente

Essayons d'obtenir l'équation de la tangente au graphe d'une fonction f au point A(x0; f(x0)). L'équation d'une droite de pente k a la forme suivante :

Puisque notre pente est égale à la dérivée f'(x0), alors l'équation prendra la forme suivante : y = f'(x0)*x + b.

Calculons maintenant la valeur de b. Pour ce faire, on utilise le fait que la fonction passe par le point A.

f(x0) = f’(x0)*x0 + b, à partir de là nous exprimons b et obtenons b = f(x0) - f’(x0)*x0.

Nous substituons la valeur résultante dans l'équation de tangente :

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Considérons l'exemple suivant: trouvez l'équation de la tangente au graphique de la fonction f (x) \u003d x 3 - 2 * x 2 + 1 au point x \u003d 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Substituez les valeurs obtenues dans la formule tangente, nous obtenons : y = 1 + 4*(x - 2). En ouvrant les parenthèses et en ramenant les mêmes termes, on obtient : y = 4*x - 7.

Réponse : y = 4*x - 7.

Schéma général de compilation de l'équation de tangente au graphique de la fonction y = f(x) :

1. Déterminez x0.

2. Calculez f(x0).

3. Calculer f'(x)

Instruction

On détermine la pente de la tangente à la courbe au point M.
La courbe représentant le graphique de la fonction y = f(x) est continue dans un certain voisinage du point M (y compris le point M lui-même).

Si la valeur f'(x0) n'existe pas, soit il n'y a pas de tangente, soit elle passe verticalement. De ce fait, la présence de la dérivée de la fonction au point x0 est due à l'existence d'une tangente non verticale qui est en contact avec le graphe de la fonction au point (x0, f(x0)). Dans ce cas, la pente de la tangente sera égale à f "(x0). Ainsi, la signification géométrique de la dérivée devient claire - le calcul de la pente de la tangente.

Trouver la valeur de l'abscisse du point de contact, qui est désignée par la lettre "a". S'il coïncide avec le point tangent donné, alors "a" sera sa coordonnée x. Déterminer la valeur les fonctions f(a), en remplaçant dans l'équation les fonctions la taille de l'abscisse.

Déterminer la dérivée première de l'équation les fonctions f'(x) et y substituer la valeur du point "a".

Prenez l'équation tangente générale, qui est définie comme y \u003d f (a) \u003d f (a) (x - a), et substituez les valeurs trouvées de a, f (a), f "( a) En conséquence, la solution du graphique sera trouvée et tangente.

Résolvez le problème d'une manière différente si le point tangent donné ne coïncidait pas avec le point tangent. Dans ce cas, il est nécessaire de substituer "a" au lieu de nombres dans l'équation tangente. Après cela, au lieu des lettres "x" et "y", substituez la valeur des coordonnées point donné. Résolvez l'équation résultante dans laquelle "a" est l'inconnue. Mettez la valeur résultante dans l'équation tangente.

Écrivez une équation pour une tangente avec la lettre "a", si l'équation est donnée dans la condition du problème les fonctions et l'équation d'une droite parallèle par rapport à la tangente désirée. Après cela, vous avez besoin d'un dérivé les fonctionsà la coordonnée au point "a". Branchez la valeur appropriée dans l'équation tangente et résolvez la fonction.

Exemple 1Étant donné une fonction F(X) = 3X 2 + 4X– 5. Écrivons l'équation de la tangente au graphe de la fonction F(X) au point du graphique avec l'abscisse X 0 = 1.

La solution. Fonction dérivée F(X) existe pour tout x R . Trouvons-le :

= (3X 2 + 4X– 5)′ = 6 X + 4.

Alors F(X 0) = F(1) = 2; (X 0) = = 10. L'équation tangente a la forme :

y = (X 0) (X – X 0) + F(X 0),

y = 10(X – 1) + 2,

y = 10X – 8.

Réponse. y = 10X – 8.

Exemple 2Étant donné une fonction F(X) = X 3 – 3X 2 + 2X+ 5. Écrivons l'équation de la tangente au graphique de la fonction F(X), parallèle à la ligne y = 2X – 11.

La solution. Fonction dérivée F(X) existe pour tout x R . Trouvons-le :

= (X 3 – 3X 2 + 2X+ 5)′ = 3 X 2 – 6X + 2.

Puisque la tangente au graphe de la fonction F(X) au point d'abscisse X 0 est parallèle à la droite y = 2X– 11, alors sa pente vaut 2, soit ( X 0) = 2. Trouver cette abscisse à partir de la condition que 3 X– 6X 0 + 2 = 2. Cette égalité n'est valable que pour X 0 = 0 et X 0 = 2. Puisque dans les deux cas F(X 0) = 5, puis la droite y = 2X + b touche le graphique de la fonction soit au point (0; 5) soit au point (2; 5).

Dans le premier cas, l'égalité numérique est vraie 5 = 2×0 + b, où b= 5, et dans le second cas, l'égalité numérique est vraie 5 = 2 × 2 + b, où b = 1.

Il y a donc deux tangentes y = 2X+ 5 et y = 2X+ 1 au graphique de la fonction F(X) parallèle à la droite y = 2X – 11.

Réponse. y = 2X + 5, y = 2X + 1.

Exemple 3Étant donné une fonction F(X) = X 2 – 6X+ 7. Écrivons l'équation de la tangente au graphique de la fonction F(X) passant par le point UN (2; –5).

La solution. Car F(2) –5, puis le point UN n'appartient pas au graphe de la fonction F(X). Laisser X 0 - abscisse du point de contact.

Fonction dérivée F(X) existe pour tout x R . Trouvons-le :

= (X 2 – 6X+ 1)′ = 2 X – 6.

Alors F(X 0) = X– 6X 0 + 7; (X 0) = 2X 0 - 6. L'équation tangente a la forme :

y = (2X 0 – 6)(X – X 0) + X– 6X+ 7,

y = (2X 0 – 6)X– X+ 7.

Depuis le point UN appartient à la tangente, alors l'égalité numérique est vraie

–5 = (2X 0 – 6)×2– X+ 7,

où X 0 = 0 ou X 0 = 4. Cela signifie que par le point UN il est possible de tracer deux tangentes au graphe de la fonction F(X).

Si un X 0 = 0, alors l'équation tangente a la forme y = –6X+ 7. Si X 0 = 4, alors l'équation tangente a la forme y = 2X – 9.

Réponse. y = –6X + 7, y = 2X – 9.

Exemple 4 Fonctions données F(X) = X 2 – 2X+ 2 et g(X) = –X 2 - 3. Écrivons l'équation de la tangente commune aux graphiques de ces fonctions.

La solution. Laisser X 1 - abscisse du point de contact de la ligne désirée avec le graphique de la fonction F(X), un X 2 - abscisse du point de contact de la même ligne avec le graphique de la fonction g(X).

Fonction dérivée F(X) existe pour tout x R . Trouvons-le :

= (X 2 – 2X+ 2)′ = 2 X – 2.

Alors F(X 1) = X– 2X 1 + 2; (X 1) = 2X 1 - 2. L'équation tangente a la forme :

y = (2X 1 – 2)(X – X 1) + X– 2X 1 + 2,

y = (2X 1 – 2)X – X+ 2. (1)

Trouvons la dérivée de la fonction g(X):

= (–X 2 – 3)′ = –2 X.

Soit une fonction f donnée, qui à un certain point x 0 a une dérivée finie f (x 0). Alors la droite passant par le point (x 0; f (x 0)), qui a une pente f '(x 0), est appelée une tangente.

Mais que se passe-t-il si la dérivée au point x 0 n'existe pas ? Il y a deux options :

1. La tangente au graphe n'existe pas non plus. L'exemple classique est la fonction y = |x | au point (0; 0).
2. La tangente devient verticale. C'est le cas, par exemple, pour la fonction y = arcsin x au point (1; π /2).

Équation tangente

Toute droite non verticale est donnée par une équation de la forme y = kx + b, où k est la pente. La tangente ne fait pas exception, et pour composer son équation en un point x 0, il suffit de connaître la valeur de la fonction et la dérivée en ce point.

Donc, donnons une fonction y \u003d f (x), qui a une dérivée y \u003d f '(x) sur le segment. Alors en tout point x 0 ∈ (a; b) une tangente peut être tracée au graphe de cette fonction, qui est donnée par l'équation :

y \u003d f '(x 0) (x - x 0) + f (x 0)

Ici f ’(x 0) est la valeur de la dérivée au point x 0, et f (x 0) est la valeur de la fonction elle-même.

Une tâche. Soit une fonction y = x 3 . Écrivez une équation pour la tangente au graphique de cette fonction au point x 0 = 2.

Équation tangente: y \u003d f '(x 0) (x - x 0) + f (x 0). Le point x 0 = 2 nous est donné, mais les valeurs f (x 0) et f '(x 0) devront être calculées.

Trouvons d'abord la valeur de la fonction. Tout est facile ici : f (x 0) = f (2) = 2 3 = 8 ;
Trouvons maintenant la dérivée: f '(x) \u003d (x 3) ' \u003d 3x 2;
Remplacez dans la dérivée x 0 = 2 : f '(x 0) = f '(2) = 3 2 2 = 12 ;
On obtient donc : y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
C'est l'équation tangente.

Une tâche. Composez l'équation de la tangente au graphique de la fonction f (x) \u003d 2sin x + 5 au point x 0 \u003d π / 2.

Cette fois, nous ne décrirons pas en détail chaque action - nous indiquerons uniquement les étapes clés. Nous avons:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

Équation tangente :

y = 0 (x − π /2) + 7 ⇒ y = 7

Dans ce dernier cas, la ligne s'est avérée horizontale, car sa pente k = 0. Il n'y a rien de mal à cela - nous sommes juste tombés sur un point extrême.