Numerele naturale pot fi folosite pentru numărare (un măr, două mere etc.)

numere întregi(din lat. naturalis- naturala; numere naturale) - numere care apar în mod natural la numărare (de exemplu, 1, 2, 3, 4, 5 ...). Se numește șirul tuturor numerelor naturale dispuse în ordine crescătoare natural unul lângă altul.

Există două abordări ale definiției numerelor naturale:

• numărare (numerotare) articole ( primul, al doilea, al treilea, Al patrulea, a cincea"…);
• numere naturale – numere care apar atunci când desemnarea cantității articole ( 0 articole, 1 articol, 2 articole, 3 articole, 4 articole, 5 articole"...).

În primul caz, seria numerelor naturale începe de la unu, în al doilea - de la zero. Nu există o opinie comună pentru majoritatea matematicienilor cu privire la preferința primei sau celei de a doua abordări (adică dacă să considerăm zero ca număr natural sau nu). Marea majoritate a surselor rusești au adoptat în mod tradițional prima abordare. A doua abordare, de exemplu, este folosită în scrierile lui Nicolas Bourbaki, unde numerele naturale sunt definite ca cardinalități ale mulțimilor finite.

Numerele negative și neîntregi (raționale, reale, ...) nu aparțin numerelor naturale.

Mulțimea tuturor numerelor naturale se obișnuiește să se desemneze simbolul N (\displaystyle \mathbb (N) ) (din lat. naturalis- naturale). Mulțimea numerelor naturale este infinită, deoarece pentru orice număr natural n (\displaystyle n) există un număr natural mai mare decât n (\displaystyle n) .

Prezența zeroului facilitează formularea și demonstrarea multor teoreme în aritmetica numerelor naturale, astfel că prima abordare introduce noțiunea utilă serie naturală extinsă, inclusiv zero. Rândul extins este notat cu N 0 (\displaystyle \mathbb (N) _(0)) sau Z 0 (\displaystyle \mathbb (Z) _(0)) .

Axiome care fac posibila definirea multimii numerelor naturale

Axiome Peano pentru numere naturale

Articolul principal: Axiomele lui Peano

O mulțime N (\displaystyle \mathbb (N) ) va fi numită o mulțime de numere naturale dacă un element este fix 1 (unul) aparținând lui N (\displaystyle \mathbb (N) ) (1 ∈ N (\displaystyle 1\in \mathbb (N) )) și o funcție S (\displaystyle S) cu domeniul N (\displaystyle \mathbb (N) ) și intervalul N (\displaystyle \mathbb (N) ) (numită funcție de succesiune; S: N → N (\displaystyle S\colon \mathbb (N) \to \mathbb (N) )) astfel încât sunt îndeplinite următoarele condiții:

1. unitatea este un număr natural (1 ∈ N (\displaystyle 1\in \mathbb (N) ));
2. numărul care urmează unui număr natural este de asemenea natural (dacă x ∈ N (\displaystyle x\in \mathbb (N) ) , atunci S (x) ∈ N (\displaystyle S(x)\in \mathbb (N) )) ;
3. nu urmează niciun număr natural (∄ x ∈ N (S (x) = 1) (\displaystyle \nexists x\in \mathbb (N) \ (S(x)=1))));
4. dacă numărul natural a (\displaystyle a) urmează imediat atât numărului natural b (\displaystyle b) cât și numărului natural c (\displaystyle c) , atunci b = c (\displaystyle b=c) (dacă S (b) = a ( \displaystyle S(b)=a) și S (c) = a (\displaystyle S(c)=a) , apoi b = c (\displaystyle b=c));
5. (axioma inducției) dacă orice propoziție (enunț) P (\displaystyle P) este dovedită pentru un număr natural n = 1 (\displaystyle n=1) ( bază de inducție) și dacă ipoteza că este adevărată pentru un alt număr natural n (\displaystyle n) implică că este adevărată pentru numărul natural care urmează pe n (\displaystyle n) ( ipoteza de inducție), atunci această propoziție este adevărată pentru toate numerele naturale (fie P (n) (\displaystyle P(n)) un predicat (unar) cu un singur loc al cărui parametru este un număr natural n (\displaystyle n) . Atunci, dacă P (1) (\displaystyle P(1)) și ∀ n (P (n) ⇒ P (S (n))) (\displaystyle \forall n\;(P(n)\Rightarrow P(S(n)) ))) , apoi ∀ n P (n) (\displaystyle \forall n\;P(n))).

Axiomele de mai sus reflectă înțelegerea noastră intuitivă a seriei naturale și a dreptei numerice.

Faptul fundamental este că aceste axiome determină în mod esențial în mod unic numerele naturale (natura categorială a sistemului de axiome ale lui Peano). Și anume, se poate dovedi (vezi și demonstrația scurtă) că dacă (N , 1 , S) (\displaystyle (\mathbb (N) ,1,S)) și (N ~ , 1 ~ , S ~) (\displaystyle ( (\tilde (\mathbb (N) )),(\tilde (1)),(\tilde (S)))) sunt două modele pentru sistemul de axiome Peano, atunci ele sunt neapărat izomorfe, adică există o mapare inversabilă (bijecție) f: N → N ~ (\displaystyle f\colon \mathbb (N) \to (\tilde (\mathbb (N) ))) astfel încât f (1) = 1 ~ (\displaystyle f( 1) =(\tilde (1))) și f (S (x)) = S ~ (f (x)) (\displaystyle f(S(x))=(\tilde (S))(f(x)) ) pentru toate x ∈ N (\displaystyle x\in \mathbb (N) ) .

Prin urmare, este suficient să fixăm ca N (\displaystyle \mathbb (N) ) orice model specific al mulțimii de numere naturale.

Definiția teoretică a mulțimilor a numerelor naturale (definiția Frege-Russell)

Conform teoriei mulțimilor, singurul obiect al construcției oricăror sisteme matematice este mulțimea.

Astfel, sunt introduse și numerele naturale, pe baza conceptului de mulțime, după două reguli:

• S (n) = n ∪ ( n ) (\displaystyle S(n)=n\cup \left\(n\right\)) .

Numerele definite în acest fel sunt numite ordinale.

Să descriem primele câteva numere ordinale și numerele lor naturale corespunzătoare:

• 0 = ∅ (\displaystyle 0=\varnothing ) ;
• 1 = ( 0 ) = ( ∅ ) (\displaystyle 1=\left\(0\right\)=\left\(\varnothing \right\)) ;
• 2 = ( 0 , 1 ) = ( ∅ , ( ∅ ) ) (\displaystyle 2=\left\(0,1\right\)=(\big \()\varnothing ,\;\left\(\varnothing \) dreapta\)(\mare \))) ;
• 3 = ( 0 , 1 , 2 ) = ( ∅ , ( ∅ ) , ( ∅ , ( ∅ ) ) ) (\displaystyle 3=\left\(0,1,2\right\)=(\Big \() \varnothing ,\;\left\(\varnothing \right\),\;(\big \()\varnothing ,\;\left\(\varnothing \right\)(\big \))(\Big \) )) .

Zero ca număr natural

Uneori, mai ales în literatura străină și tradusă, prima și a treia axiomă a lui Peano înlocuiesc una cu zero. În acest caz, zero este considerat un număr natural. Când este definit în termeni de clase de mulțimi echivalente, zero este un număr natural prin definiție. Ar fi nefiresc să-l aruncăm în mod specific. În plus, acest lucru ar complica semnificativ construcția și aplicarea ulterioară a teoriei, deoarece în majoritatea construcțiilor zero, precum mulțimea goală, nu este ceva izolat. Un alt avantaj de a considera zero ca număr natural este că N (\displaystyle \mathbb (N) ) formează un monoid.

În literatura rusă, zero este de obicei exclus din numărul de numere naturale (0 ∉ N (\displaystyle 0\notin \mathbb (N) )), iar mulțimea numerelor naturale cu zero este notată ca N 0 (\displaystyle \mathbb (N) _(0) ). Dacă zero este inclus în definiția numerelor naturale, atunci mulțimea numerelor naturale este scrisă ca N (\displaystyle \mathbb (N) ) și fără zero - ca N ∗ (\displaystyle \mathbb (N) ^(*) ).

În literatura matematică internațională, ținând cont de cele de mai sus și pentru a evita ambiguitățile, mulțimea ( 1 , 2 , … ) (\displaystyle \(1,2,\dots \)) este de obicei numită mulțime de numere întregi pozitive și notată cu Z + (\displaystyle \ mathbb (Z) _(+)) . Mulțimea ( 0 , 1 , … ) (\displaystyle \(0,1,\dots \)) este adesea numită mulțimea de numere întregi nenegative și notat cu Z ⩾ 0 (\displaystyle \mathbb (Z) _(\ geqslant 0)) .

Poziția mulțimii de numere naturale (N (\displaystyle \mathbb (N) )) printre mulțimile de numere întregi (Z (\displaystyle \mathbb (Z) )), numere raționale (Q (\displaystyle \mathbb (Q) ) ) ), numere reale (R (\displaystyle \mathbb (R) )) și numere iraționale (R ∖ Q (\displaystyle \mathbb (R) \setminus \mathbb (Q) ))

Valoarea mulțimii numerelor naturale

Mărimea unei mulțimi infinite este caracterizată de conceptul de „putere a unei mulțimi”, care este o generalizare a numărului de elemente ale unei mulțimi finite la mulțimi infinite. În mărime (adică cardinalitate), mulțimea numerelor naturale este mai mare decât orice mulțime finită, dar mai mică decât orice interval, de exemplu, intervalul (0 , 1) (\displaystyle (0,1)) . Mulțimea numerelor naturale are aceeași cardinalitate ca și mulțimea numerelor raționale. O mulțime de aceeași cardinalitate ca și mulțimea numerelor naturale se numește mulțime numărabilă. Astfel, setul de termeni ai oricărei secvențe este numărabil. În același timp, există o succesiune în care fiecare număr natural apare de un număr infinit de ori, deoarece mulțimea numerelor naturale poate fi reprezentată ca o uniune numărabilă de mulțimi numărabile disjunse (de exemplu, N = ⋃ k = 0 ∞ ( ⋃ n = 0 ∞ (2 n + 1) 2 k) (\displaystyle \mathbb (N) =\bigcup \limits _(k=0)^(\infty)\left(\bigcup \limits _(n=0) )^(\infty )(2n+ 1)2^(k)\dreapta))).

Operatii pe numere naturale

Operațiile închise (operațiile care nu scot un rezultat din setul de numere naturale) pe numere naturale includ următoarele operații aritmetice:

• plus: termen + termen = suma;
• multiplicare: multiplicator × multiplicator = produs;
• exponentiare: a b (\displaystyle a^(b)) , unde a (\displaystyle a) este baza exponentului, b (\displaystyle b) este exponentul. Dacă a (\displaystyle a) și b (\displaystyle b) sunt numere naturale, atunci rezultatul este și un număr natural.

În plus, sunt luate în considerare încă două operații (din punct de vedere formal, nu sunt operații pe numere naturale, deoarece nu sunt definite pentru toate perechi de numere (uneori există, alteori nu)):

• scădere: minuend - subtrahend = diferenta. În acest caz, minuendul trebuie să fie mai mare decât subtraend (sau egal cu acesta, dacă considerăm zero ca număr natural);
• împărțire cu rest: dividend / divizor = (cot, rest). Coeficientul p (\displaystyle p) și restul r (\displaystyle r) când a (\displaystyle a) este împărțit la b (\displaystyle b) sunt definite după cum urmează: a = p ⋅ b + r (\displaystyle a= p\cdot b+ r) și 0 ⩽ r b (\displaystyle 0\leqslant r poate fi reprezentat ca a = p ⋅ 0 + a (\displaystyle a=p\cdot 0+a) , adică orice număr ar putea fi considerat privat, iar restul a (\displaystyle a) .

De remarcat că operațiile de adunare și înmulțire sunt fundamentale. În special, inelul numerelor întregi este definit tocmai prin operațiile binare de adunare și înmulțire.

Proprietăți de bază

• Comutativitatea adunării:

a + b = b + a (\displaystyle a+b=b+a) .

• Comutativitatea înmulțirii:

a ⋅ b = b ⋅ a (\displaystyle a\cdot b=b\cdot a) .

• Asociativitatea adunării:

(a + b) + c = a + (b + c) (\displaystyle (a+b)+c=a+(b+c)) .

• Asociativitatea înmulțirii:

(a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) (\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c)) .

• Distributivitatea înmulțirii în raport cu adunarea:

( a ⋅ (b + c) = a ⋅ b + a ⋅ c (b + c) ⋅ a = b ⋅ a + c ⋅ a (\displaystyle (\begin(cases)a\cdot (b+c)=a \cdot b+a\cdot c\\(b+c)\cdot a=b\cdot a+c\cdot a\end(cases))) .

Structura algebrică

Adunarea transformă mulțimea numerelor naturale într-un semigrup cu unitate, rolul unității este jucat de 0 . Înmulțirea transformă și mulțimea numerelor naturale într-un semigrup cu unitate, în timp ce elementul de identitate este 1 . Încheind operațiile de adunare-scădere și înmulțire-împărțire, obținem grupuri de numere întregi Z (\displaystyle \mathbb (Z) ) și numere pozitive raționale Q + ∗ (\displaystyle \mathbb (Q) _(+)^(*)) respectiv.

Definiții teoretice de mulțimi

Să folosim definiția numerelor naturale ca clase de echivalență de mulțimi finite. Dacă notăm clasa de echivalență a unei mulțimi A, generat prin bijecții, folosind paranteze drepte: [ A], operațiile aritmetice de bază sunt definite după cum urmează:

• [ A ] + [ B ] = [ A ⊔ B ] (\displaystyle [A]+[B]=) ;
• [ A ] ⋅ [ B ] = [ A × B ] (\displaystyle [A]\cdot [B]=) ;
• [ A ] [ B ] = [ A B ] (\displaystyle ([A])^([B])=) ,

• A ⊔ B (\displaystyle A\sqcup B) - uniunea disjunctă de mulțimi;
• A × B (\displaystyle A\times B) - produs direct;
• A B (\displaystyle A^(B)) - set de afișaje din Bîn A.

Se poate arăta că operațiile rezultate pe clase sunt introduse corect, adică nu depind de alegerea elementelor de clasă și coincid cu definițiile inductive.

Ce este un număr natural? Istorie, domeniu de aplicare, proprietăți

Matematica a apărut din filosofia generală în jurul secolului al VI-lea î.Hr. e., iar din acel moment a început marșul ei victorios în jurul lumii. Fiecare etapă de dezvoltare a introdus ceva nou – numărătoarea elementară a evoluat, s-a transformat în calcul diferențial și integral, secolele s-au schimbat, formulele au devenit din ce în ce mai confuze, iar a venit momentul în care „a început cea mai complexă matematică – toate numerele au dispărut din ea”. Dar care a fost baza?

Începutul timpului

Numerele naturale au apărut odată cu primele operații matematice. Odată o coloană vertebrală, doi țepi, trei țepi... Au apărut datorită oamenilor de știință indieni care au dezvoltat primul sistem de numere poziționale.
Cuvântul „poziționalitate” înseamnă că locația fiecărei cifre dintr-un număr este strict definită și corespunde categoriei sale. De exemplu, numerele 784 și 487 sunt aceleași numere, dar numerele nu sunt echivalente, deoarece primul include 7 sute, în timp ce al doilea doar 4. Arabii au preluat inovația indienilor, care au adus numerele la forma pe care îl știm acum.

În antichitate, se dădeau numere sens mistic, cel mai mare matematician Pitagora credea că numărul stă la baza creării lumii împreună cu elementele de bază - foc, apă, pământ, aer. Dacă luăm în considerare totul doar din partea matematică, atunci ce este un număr natural? Câmpul numerelor naturale se notează cu N și este o serie infinită de numere care sunt întregi și pozitive: 1, 2, 3, … + ∞. Zero este exclus. Este folosit în principal pentru numărarea articolelor și indicarea comenzii.

Ce este un număr natural în matematică? Axiomele lui Peano

Câmpul N este câmpul de bază pe care se bazează matematica elementară. De-a lungul timpului, s-au distins câmpurile numerelor întregi, raționale, complexe.

Lucrarea matematicianului italian Giuseppe Peano a făcut posibilă structurarea ulterioară a aritmeticii, a atins formalitatea acesteia și a deschis calea pentru concluzii ulterioare care au depășit domeniul N. Ce este un număr natural, s-a aflat mai devreme limbaj simplu, definiția matematică bazată pe axiomele lui Peano va fi luată în considerare mai jos.

• Unul este considerat un număr natural.
• Numărul care urmează unui număr natural este un număr natural.
• Nu există un număr natural înainte de unu.
• Dacă numărul b urmează atât numărul c cât și numărul d, atunci c=d.
• Axioma inducției, care la rândul ei arată ce este un număr natural: dacă o afirmație care depinde de un parametru este adevărată pentru numărul 1, atunci presupunem că funcționează și pentru numărul n din câmpul numerelor naturale N. Atunci afirmația este valabilă și pentru n =1 din câmpul numerelor naturale N.

Operații de bază pentru domeniul numerelor naturale

Deoarece câmpul N a devenit primul pentru calcule matematice, atât domeniile de definiție, cât și intervalele de valori ale unui număr de operații de mai jos se referă la el. Sunt inchise si nu. Principala diferență este că operațiunile închise sunt garantate pentru a lăsa un rezultat în mulțimea N, indiferent de numerele implicate. Este suficient ca sunt naturale. Rezultatul interacțiunilor numerice rămase nu mai este atât de clar și depinde direct de ce fel de numere sunt implicate în expresie, deoarece poate contrazice definiția principală. Deci, operațiuni închise:

• adunarea – x ​​+ y = z, unde x, y, z sunt incluse în câmpul N;
• înmulțire - x * y = z, unde x, y, z sunt incluse în câmpul N;
• exponentiație - xy, unde x, y sunt incluse în câmpul N.

Operațiunile rămase, al căror rezultat poate să nu existe în contextul definiției „ce este un număr natural”, sunt următoarele:

Proprietățile numerelor aparținând câmpului N

Toate raționamentele matematice ulterioare se vor baza pe următoarele proprietăți, cele mai banale, dar nu mai puțin importante.

• Proprietatea comutativă a adunării este x + y = y + x, unde numerele x, y sunt incluse în câmpul N. Sau binecunoscutul „suma nu se modifică dintr-o modificare a locurilor termenilor”.
• Proprietatea comutativă a înmulțirii este x * y = y * x, unde numerele x, y sunt incluse în câmpul N.
• Proprietatea asociativă a adunării este (x + y) + z = x + (y + z), unde x, y, z sunt incluse în câmpul N.
• Proprietatea asociativă a înmulțirii este (x * y) * z = x * (y * z), unde numerele x, y, z sunt incluse în câmpul N.
• proprietatea distribuției - x (y + z) = x * y + x * z, unde numerele x, y, z sunt incluse în câmpul N.

Masa lui Pitagora

Unul dintre primii pași în cunoașterea întregii structuri a matematicii elementare de către școlari, după ce au înțeles singuri care numere sunt numite naturale, este tabelul lui Pitagora. Poate fi considerat nu numai din punct de vedere al științei, ci și ca un monument științific valoros.

Această masă de înmulțire a suferit o serie de modificări de-a lungul timpului: zero a fost eliminat din ea, iar numerele de la 1 la 10 se desemnează, fără a ține cont de ordine (sute, mii...). Este un tabel în care titlurile rândurilor și coloanelor sunt numere, iar conținutul celulelor intersecției lor este egal cu produsul lor.

În practica predării din ultimele decenii, a fost nevoie de memorarea tabelului pitagoreic „în ordine”, adică memorarea a fost prima. Înmulțirea cu 1 a fost exclusă deoarece rezultatul a fost 1 sau mai mare. Între timp, în tabelul cu ochiul liber, puteți vedea un model: produsul numerelor crește cu un pas, care este egal cu titlul liniei. Astfel, al doilea factor ne arată de câte ori trebuie să-l luăm pe primul pentru a obține produsul dorit. Acest sistem spre deosebire de cel care se practica în Evul Mediu: chiar și înțelegând ce este un număr natural și cât de banal este, oamenii au reușit să-și complice numărarea de zi cu zi folosind un sistem bazat pe puterile a doi.

Subset ca leagăn al matematicii

Pe acest moment domeniul numerelor naturale N este considerat doar una dintre submulțimile numerelor complexe, dar acest lucru nu le face mai puțin valoroase în știință. Numărul natural este primul lucru pe care îl învață un copil studiindu-se pe sine și lumea. Un deget, două degete... Datorită lui, se formează o persoană gandire logica, precum și capacitatea de a determina cauza și de a deduce efectul, deschizând calea unor mari descoperiri.

Discuție: Număr natural

Controversa în jurul zero

Din anumite motive, nu-mi pot imagina zero ca număr natural... Se pare că anticii nu știau zero deloc. Da, iar TSB nu consideră zero un număr natural. Deci prin macar aceasta este o declarație controversată. Poți spune ceva mai neutru despre zero? Sau există argumente bune? --.:Ajvol:. 18:18, 9 septembrie 2004 (UTC)

S-a anulat ultima modificare. --Maxal 20:24 9 septembrie 2004 (UTC)

Academia Franceză a emis odată un decret special conform căruia 0 era inclus în setul de numere naturale. Acum, acesta este standardul, în opinia mea, nu este necesar să se introducă conceptul de „număr natural rus”, ci să adere la acest standard. Desigur, trebuie menționat că odată nu a fost așa (nu numai în Rusia, ci peste tot). Tosha 23:16, 9 septembrie 2004 (UTC)

Academia Franceză nu este un decret pentru noi. În literatura de matematică în limba engleză, nu există nici o opinie stabilită în această privință. Vedeți, de exemplu, --Maxal 23:58, 9 septembrie 2004 (UTC)

Undeva acolo scrie: „Dacă scrieți un articol despre o problemă controversată, atunci încercați să prezentați toate punctele de vedere, oferind link-uri către opinii diferite.". Insula Bes 23:15, 25 decembrie 2004 (UTC)

Nu văd o problemă controversată aici, dar văd: 1) lipsă de respect față de ceilalți participanți prin schimbarea / ștergerea semnificativă a textului lor (se obișnuiește să le discutăm înainte de a face modificări semnificative); 2) înlocuirea definițiilor stricte (care indică cardinalitățile mulțimilor) cu cele indistincte (există o diferență mare între „numerotare” și „notația cantității”?). Prin urmare, refac un rollback, totuși, las o ultimă observație. --Maxal 23:38, 25 decembrie 2004 (UTC)

Lipsa de respect este exact felul în care văd împotrivirile tale. Deci să nu vorbim despre asta. Editarea mea nu schimbă esența articol, formulează clar doar două definiții. Versiunea anterioară a articolului a formulat definiția „fără zero” ca principală, iar „cu zero” ca un fel de disidență. Acest lucru nu îndeplinește absolut cerințele Wikipedia (vezi citatul de mai sus), precum și nu chiar stilul științific declarații din versiunea anterioară. Am adăugat formularea „cardinalitate a unui set” ca explicație pentru „desemnarea cantității” și „enumerare” pentru „numerotare”. Și dacă nu vedeți diferența dintre „numerotare” și „desemnarea cantității”, atunci, lăsați-mă să vă întreb, de ce atunci editați articole matematice? Insula Bes 23:58, 25 decembrie 2004 (UTC)

În ceea ce privește „nu schimbă esența” - versiunea anterioară a subliniat că diferența dintre definiții este doar în referirea zero la numere naturale. În versiunea dvs., definițiile sunt prezentate ca fiind radical diferite. În ceea ce privește definiția „de bază”, atunci ar trebui să fie așa, deoarece acest articol în Rusă Wikipedia, ceea ce înseamnă că practic trebuie să rămâi la ceea ce spui comună în rusă scoli de matematica . Ignor raidurile. --Maxal 00:15, 26 decembrie 2004 (UTC)

De fapt, aceasta este doar o diferență de numai zero. De fapt, aceasta este tocmai diferența cardinală care vine dintr-o înțelegere diferită a naturii numerelor naturale: într-o versiune - ca cantități; în celălalt – ca numere. aceasta absolut concepte diferite oricât ai încerca să ascunzi că nu înțelegi.

Despre faptul că în Wikipedia rusă se cere să se citeze punctul de vedere rus ca fiind dominant. Privește cu atenție aici. Uită-te la articolul în limba engleză despre Crăciun. Nu spune că Crăciunul ar trebui sărbătorit pe 25 decembrie, pentru că așa îl sărbătoresc în Anglia și SUA. Ambele puncte de vedere sunt date acolo (și diferă nici mai mult, nici mai puțin decât numerele naturale „cu zero” și „fără zero” diferă), și nici măcar un cuvânt despre care dintre ele se presupune că este mai corect.

În versiunea mea a articolului, ambele puncte de vedere sunt desemnate ca independente și la fel de valabile. Standardul rusesc este indicat de cuvintele la care v-ați referit mai sus.

Poate că, din punct de vedere filozofic, conceptele de numere naturale sunt într-adevăr absolut diferit, dar articolul oferă definiții în esență matematice, unde diferența este 0 ∈ N (\displaystyle 0\in \mathbb (N) ) sau 0 ∉ N (\displaystyle 0\not \in \mathbb (N) ) . Punctul de vedere dominant sau nu este o chestiune delicată. Apreciez fraza observat în cea mai mare parte a lumii occidentale la 25 decembrie din articolul în limba engleză despre Crăciun ca exprimând punctul de vedere dominant, fără alte date date în primul paragraf. Apropo, în versiunea anterioară a articolului despre numerele naturale nu existau nici indicii directe despre cum necesar pentru a determina numerele naturale, doar o definiție fără zero a fost prezentată ca fiind mai comună (în Rusia). În orice caz, e bine că s-a găsit un compromis. --Maxal 00:53, 26 decembrie 2004 (UTC)

Expresia „În literatura rusă, zero este de obicei exclus din numărul de numere naturale” este oarecum neplăcut surprinzătoare, domnilor, zero nu este considerat un număr natural, dacă nu se specifică altfel, în întreaga lume. Aceeași franceză, din câte le-am citit, stipulează în mod specific includerea lui zero. Desigur, N 0 (\displaystyle \mathbb (N) _(0)) este folosit mai des, dar dacă, de exemplu, îmi plac femeile, nu voi schimba bărbații în femei. Druid. 23-02-2014

Impopularitatea numerelor naturale

Mi se pare că numerele naturale sunt un subiect nepopular în articolele de matematică (poate nu în ultimul rând din cauza lipsei unei definiții unice). Din experiența mea, întâlnesc adesea termenii din articolele de matematică numere întregi nenegativeși numere întregi pozitive(care sunt interpretate fără ambiguitate) decât numere întregi. Părțile interesate sunt rugate să își exprime (dez)acordul cu această observație. Dacă această observație găsește sprijin, atunci este logic să o indicați în articol. --Maxal 01:12, 26 decembrie 2004 (UTC)

Fără îndoială, ai dreptate în partea rezumată a declarației tale. Totul se datorează diferențelor de definiție. Eu însumi prefer în unele cazuri să indică „numere întregi pozitive” sau „numere întregi nenegative” în loc de „naturale” pentru a evita discrepanțe în ceea ce privește includerea lui zero. Și în general sunt de acord cu dispozitivul. Insula Bes 01:19, 26 Dec 2004 (UTC) În articole - da, poate că este. Cu toate acestea, în textele mai voluminoase, precum și în cazul în care conceptul este folosit des, de obicei se folosesc în continuare numere întregi, preliminar, însă, explicând „despre ce” numere naturale vorbim – cu sau fără zero. LoKi 19:31 30 iulie 2005 (UTC)

Numerele

Merită să enumerați numele numerelor (unu, doi, trei etc.) în ultima parte a acestui articol? Nu ar avea mai mult sens să pun asta în articolul Number? Totuși, acest articol, în opinia mea, ar trebui să fie mai de natură matematică. Cum crezi? --LoKi 19:32, 30 iulie 2005 (UTC)

În general, este ciudat cum este posibil să obțineți un număr natural obișnuit din mulțimi *vide*? În general, câte goluri și goluri nu se combină, cu excepția golului, nimic nu va funcționa! Nu este deloc o definiție alternativă? Postat la 21:46, 17 iulie 2009 (Moscova)

Natura categorica a sistemului de axiome lui Peano

Am adăugat o remarcă despre natura categorială a sistemului axiomelor lui Peano, care, după părerea mea, este fundamentală. Formatați corect linkul către carte[[Utilizator:A_Devyatkov 06:58, 11 iunie 2010 (UTC)]]

Axiomele lui Peano

În aproape toată literatura străină și pe Wikipedia, axiomele lui Peano încep cu „0 este un număr natural”. Într-adevăr, în sursa originală este scris „1 este un număr natural”. Cu toate acestea, în 1897 Peano a făcut o schimbare și a schimbat 1 la 0. Aceasta este scrisă în „Formulaire de mathematiques”, Volumul II - Nr. 2. pagina 81. Acesta este un link către versiunea electronică de pe pagina din dreapta:

http://archive.org/stream/formulairedemat02peangoog#page/n84/mode/2up (fr).

Explicațiile acestor modificări sunt date în „Rivista di matematica”, Vol. 6-7, 1899, pag. 76. De asemenea, un link către versiunea electronică pe pagina din dreapta:

http://archive.org/stream/rivistadimatema01peangoog#page/n69/mode/2up (italiană).

0=0

Care sunt „axiomele platourilor digitale”?

Aș dori să returnez articolul la cea mai recentă versiune de patrulare. În primul rând, cineva a redenumit axiomele lui Peano în axiomele lui Piano, din cauza cărora legătura a încetat să funcționeze. În al doilea rând, un anume Curd a adăugat articolului o informație foarte mare, care, după părerea mea, este complet nepotrivită în acest articol. Scris neenciclopedic, în plus, sunt oferite rezultatele lui Tvorogov însuși și un link către propria sa carte. Insist ca secțiunea despre „axiomele plăcilor digitale” să fie eliminată din acest articol. P.s. De ce a fost eliminată secțiunea despre numărul zero? mesyarik 14:58, 12 martie 2014 (UTC)

Subiectul nu este dezvăluit, este necesară o definiție clară a numerelor naturale

Te rog nu scrie erezie ca " Numere naturale (numere naturale) - numere care apar în mod natural la numărare.„În mod natural, nimic nu apare în creier. Va fi exact ceea ce vei pune acolo.

Și pentru un copil de cinci ani, cum să explic ce număr este un număr natural? La urma urmei, există oameni care trebuie explicați ca fiind un copil de cinci ani. Cum este un număr natural diferit de un număr obișnuit? Sunt necesare exemple! 1, 2, 3 este natural și 12 este natural și -12? și trei sferturi, sau de exemplu 4,25 naturale? 95.181.136.132 15:09 6 noiembrie 2014 (UTC)

• Numerele naturale sunt un concept fundamental, o abstractizare inițială. Ele nu pot fi definite. Puteți intra în mod arbitrar adânc în filozofie, dar în cele din urmă fie trebuie să recunoașteți (o luați pe credință?) O atitudine metafizică rigidă, fie să recunoașteți că nu există o definiție absolută, numerele naturale fac parte dintr-un sistem formal artificial, un model. care a fost inventat de o persoană (sau Dumnezeu). Iată un tratat interesant pe această temă. Cum vă place, de exemplu, această opțiune: „O serie naturală este orice sistem Peano specific, adică un model al teoriei axiomatice a lui Peano”. Te simți mai bine? RomanSuzi 17:52, 6 noiembrie 2014 (UTC)
  • Se pare că cu modelele tale și teoriile axiomatice nu faci decât să complici totul. În cel mai bun caz, doi din o mie de oameni vor înțelege o astfel de definiție. Prin urmare, cred că din primul paragraf îi lipsește propoziția " Cu cuvinte simple: numerele naturale sunt numere întregi pozitive începând de la unu inclusiv." O astfel de definiție sună normal pentru majoritatea. Și nu dă motive să ne îndoim de definiția unui număr natural. La urma urmei, după ce am citit articolul, chiar nu am înțeles până când terminați ce sunt numerele naturale și numărul 807423 este numerele naturale sau numerele naturale sunt cele din care este format acest număr, adică 8 0 7 4 2 3. Adesea complicațiile doar strica totul.Infa despre numerele naturale ar trebui să fie pe această pagină și nu în numeroasele link-uri la alte pagini.95.181.136.132 10:03, 7 noiembrie 2014 (UTC)
    • Aici este necesar să se facă distincția între două sarcini: (1) să explice clar (deși nu strict) unui cititor care este departe de matematică ce este un număr natural, astfel încât să înțeleagă mai mult sau mai puțin corect; (2) să dea o definiție atât de riguroasă a unui număr natural din care rezultă proprietățile sale de bază. Aveți dreptate în favoarea primei opțiuni din preambul, dar tocmai aceasta este dată în articol: un număr natural este o formalizare matematică a numărului: unu, doi, trei etc. Exemplul dvs. (807423) poate cu siguranță se dovedesc la numărare, ceea ce înseamnă că și acesta este un număr natural. Nu îmi este clar de ce amestecați numărul și felul în care este scris în cifre, acesta este un subiect separat, care nu are legătură directă cu definiția numărului. Explicatia ta: numerele naturale sunt numere întregi pozitive începând de la unu inclusiv» nu este bun, pentru că nu poți defini mai puțin de concept general(număr natural) printr-un (număr) mai general nedefinit încă. Îmi este greu să-mi imaginez un cititor care știe ce este un număr întreg pozitiv, dar habar nu are ce este un număr natural. LGB 12:06 7 noiembrie 2014 (UTC)
      • Numerele naturale nu pot fi definite în termeni de numere întregi. RomanSuzi 17:01, 7 noiembrie 2014 (UTC)

• „Desigur, nimic nu se întâmplă în creier.” Studii recente arată (nu pot găsi linkuri acum) că creierul uman este pregătit să folosească limbajul. Astfel, într-un mod firesc, avem deja în genele noastre disponibilitatea de a stăpâni limba. Ei bine, pentru numerele naturale, acesta este ceea ce aveți nevoie. Conceptul de „1” poate fi afișat cu o mână și apoi - prin inducție, adăugați bețe, obținând 2, 3 și așa mai departe. Sau: I, II, III, IIII, ..., IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII. Dar poate aveți sugestii specifice pentru îmbunătățirea articolului, bazate pe surse autorizate? RomanSuzi 17:57, 6 noiembrie 2014 (UTC)

Ce este un număr natural în matematică?

Vladimir Z

Numerele naturale sunt folosite pentru a enumera obiectele și pentru a număra numărul acestora. Pentru numerotare se folosesc numere întregi pozitive, începând de la 1.

Și pentru a număra numărul, aici este inclus și 0, indicând absența obiectelor.

Dacă conceptul de numere naturale conține numărul 0 depinde de axiomatică. Dacă prezentarea oricărei teorii matematice necesită prezența lui 0 în mulțimea numerelor naturale, atunci aceasta este stipulată și considerată un adevăr (axiomă) incontestabil în cadrul acestei teorii. Definiția numărului 0, atât pozitiv, cât și negativ, se apropie foarte mult de aceasta. Dacă luăm pentru definiția numerelor naturale ca mulțime a tuturor numerelor întregi NEnegative, atunci se pune întrebarea, care este numărul 0 - pozitiv sau negativ?

În aplicarea practică, se utilizează de obicei prima definiție, care nu include numărul 0.

Creion

Numerele naturale sunt numere întregi pozitive. Numerele naturale sunt folosite pentru a număra (număr) obiecte sau pentru a indica numărul de obiecte sau pentru a indica număr de serie obiect din listă. Unii autori includ în mod artificial zero în conceptul de „numere naturale”. Alții folosesc formularea „numere naturale și zero”. Acest lucru este lipsit de principii. Mulțimea numerelor naturale este infinită, deoarece cu orice număr natural arbitrar de mare, puteți efectua o operație de adunare cu un alt număr natural și puteți obține un număr și mai mare.

Numerele negative și non-întregi nu sunt incluse în setul de numere naturale.

Sayans

Numerele naturale sunt numere care sunt folosite pentru numărare. Ele pot fi doar pozitive și întregi. Ce înseamnă asta într-un exemplu? Deoarece aceste numere sunt folosite pentru numărare, să încercăm să calculăm ceva. Ce poate fi numărat? De exemplu, oamenii. Putem număra oameni astfel: 1 persoană, 2 persoane, 3 persoane etc. Numerele 1, 2, 3 și altele folosite pentru numărare vor fi naturale. Nu spunem niciodată -1 (minus unu) persoane sau 1,5 (unu și jumătate) persoane (scuze pentru jocul de cuvinte :), așa că -1 și 1,5 (ca toate numerele negative și fracționale) nu sunt numere naturale.

Lorelei

Numerele naturale sunt acele numere care sunt folosite la numărarea obiectelor.

Cel mai mic număr natural este unul. Se pune adesea întrebarea dacă zero este un număr natural. Nu, nu este în majoritatea surselor rusești, dar în alte țări numărul zero este recunoscut ca fiind natural ...

Moreljuba

Numerele naturale în matematică sunt numere folosite pentru a număra succesiv ceva sau pe cineva. Unul este considerat a fi cel mai mic număr natural. Zero în majoritatea cazurilor nu aparține categoriei numerelor naturale. Nici numerele negative nu sunt incluse aici.

Salutări slavilor.

Numerele naturale, sunt și naturale, sunt acele numere care apar în mod obișnuit atunci când sunt numărate, care sunt mai mari decât zero. Secvența fiecărui număr natural aranjat în ordine crescătoare va fi numită serie naturală.

Elena Nikityuk

Termenul de număr natural este folosit în matematică. Un număr întreg pozitiv se numește număr natural. Cel mai mic număr natural este considerat a fi „0”. Pentru a calcula orice, se folosesc aceleași numere naturale, de exemplu 1,2,3... și așa mai departe.

Numerele naturale sunt numerele cu care numărăm, adică isla unu, doi, trei, patru, cinci și altele sunt numere naturale.

Acestea sunt în mod necesar numere pozitive mai mari decât zero.

Numerele fracționale, de asemenea, nu aparțin mulțimii numerelor naturale.

-Orhidee-

Numerele naturale sunt necesare pentru a număra ceva. Sunt o serie de numere numai pozitive, începând de la unul. Este important de știut că aceste numere sunt exclusiv numere întregi. Orice poate fi numărat cu numere naturale.

Marlena

Un număr natural este un număr întreg, pe care îl folosim de obicei atunci când numărăm orice obiecte. Zero ca atare nu este inclus în domeniul numerelor naturale, deoarece de obicei nu îl folosim în calcule.

Inara-pd

Numerele naturale sunt numerele pe care le folosim pentru a număra - unu, doi, trei și așa mai departe.

Numerele naturale au apărut din nevoile practice ale omului.

Numerele naturale sunt scrise cu zece cifre.

Zero nu este un număr natural.

Ce este un număr natural?

Naumenko

Numerele se numesc numere naturale. folosit pentru numerotarea și numărarea obiectelor naturale (floare, copac, animal, pasăre etc.).

Se numesc numere întregi numerele NATURALE, ELE OPUSE ȘI ZERO,

Explica. ceea ce este natural prin numere întregi este greșit!! !

Numerele sunt pare - divizibile cu 2 și impare - nu sunt divizibile cu 2.

Numerele se numesc numere prime. având doar 2 divizori - unul și el însuși...
Prima dintre ecuațiile tale nu are soluții. pentru al doilea număr natural x=6 6.

Numere naturale (numere naturale) - numere care apar în mod natural la numărare (atât în ​​sensul de enumerare, cât și în sensul de calcul).

Mulțimea tuturor numerelor naturale este de obicei notată cu \mathbb(N). Mulțimea numerelor naturale este infinită, deoarece pentru orice număr natural există un număr natural mai mare.

Anna Semencenko

numere care apar în mod natural în timpul numărării (atât în ​​sensul de enumerare, cât și în sensul calculului).
Există două abordări ale definiției numerelor naturale - numerele utilizate în:
enumerarea (numerotarea) articolelor (primul, al doilea, al treilea, ...);
desemnarea numărului de articole (nici un articol, un articol, două articole, ...). Adoptat în lucrările lui Bourbaki, unde numerele naturale sunt definite ca puteri ale mulțimilor finite.
Numerele negative și neîntregi (raționale, reale, ...) nu sunt naturale.
Mulțimea tuturor numerelor naturale este de obicei notă printr-un semn. Mulțimea numerelor naturale este infinită, deoarece pentru orice număr natural există un număr natural mai mare.

1.1 Definiție

Sunt apelate numerele pe care oamenii le folosesc atunci când numără natural(de exemplu, unu, doi, trei, ..., o sută, o sută unu, ..., trei mii două sute douăzeci și unu, ...) Pentru a scrie numerele naturale se folosesc semne speciale (simboluri) , numit cifre.

În zilele noastre acceptat notație zecimală. Sistemul zecimal (sau modul) de scriere a numerelor folosește cifre arabe. Acestea sunt zece caractere cu cifre diferite: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Cel mai puţin un număr natural este un număr unul, ea scris cu o cifra zecimala - 1. Următorul număr natural se obține din cel anterior (cu excepția unuia) prin adăugarea a 1 (unu). Această adăugare se poate face de mai multe ori (un număr infinit de ori). Înseamnă că Nu cel mai mare numar natural. Prin urmare, se spune că seria numerelor naturale este nelimitată sau infinită, întrucât nu are sfârșit. Numerele naturale sunt scrise folosind cifre zecimale.

1.2. Numărul „zero”

Pentru a indica absența a ceva, utilizați numărul " zero" sau " zero". Se scrie cu cifre. 0 (zero). De exemplu, într-o cutie toate bilele sunt roșii. Câte dintre ele sunt verzi? - Răspuns: zero . Deci nu sunt bile verzi în cutie! Cifra 0 poate însemna că ceva s-a terminat. De exemplu, Masha a avut 3 mere. Ea a împărțit două cu prietenii, unul l-a mâncat singură. Deci ea a plecat 0 (zero) mere, i.e. niciunul ramas. Cifra 0 ar putea însemna că ceva nu s-a întâmplat. De exemplu, un meci de hochei între echipa rusă și echipa canadiană s-a încheiat cu scor 3:0 (a se citi „trei – zero”) în favoarea echipei ruse. Aceasta înseamnă că echipa rusă a marcat 3 goluri, iar echipa canadiană 0 goluri, nu a putut înscrie un singur gol. Trebuie să ne amintim că zero nu este un număr natural.

1.3. Scrierea numerelor naturale

În modul zecimal de a scrie un număr natural, fiecare cifră poate însemna numere diferite. Depinde de locul acestei cifre în notația numărului. Se numește un anumit loc în notația unui număr natural poziţie. Prin urmare, se numește notația zecimală pozițional. Luați în considerare notația zecimală 7777 a numărului şapte mii şapte sute şaptezeci şi şapte. Există șapte mii, șapte sute, șapte zeci și șapte unități în această intrare.

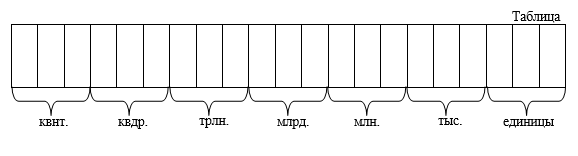
Fiecare dintre locurile (pozițiile) din notația zecimală a unui număr este numită deversare. Fiecare trei cifre sunt combinate în Clasă. Această unire se realizează de la dreapta la stânga (de la sfârșitul introducerii numărului). Diferitele ranguri și clase au propriile lor nume. Numărul de numere naturale este nelimitat. Prin urmare, numărul de ranguri și clase nu este limitat ( la nesfârşit). Luați în considerare numele cifrelor și claselor folosind exemplul unui număr cu notație zecimală

38 001 102 987 000 128 425:

Clasele și gradele
chintilioane		sute de chintilioane
		zeci de chintilioane
		chintilioane
cvadrilioane		sute de cvadrilioane
		zeci de cvadrilioane
		cvadrilioane
trilioane		sute de trilioane
		zeci de trilioane
		trilioane
miliarde		sute de miliarde
		zeci de miliarde
		miliarde
milioane		sute de milioane
		zeci de milioane
		milioane
		sute de mii
		zeci de mii

Deci, clasele, începând cu cei mai tineri, au nume: unități, mii, milioane, miliarde, trilioane, cvadrilioane, chintilioane.

1.4. Unități de biți

Fiecare dintre clasele de notare a numerelor naturale este formată din trei cifre. Fiecare rang are unități de biți. Următoarele numere sunt numite unități de biți:

1 - unitate cifră a cifrei unităților,

10 - unitatea de cifre a cifrei zecilor,

100 - unitate de biți a cifrei sutelor,

1 000 - unitate de biți a locului miilor,

10.000 - unitate de cifre de zeci de mii,

100.000 - unitate de biți de sute de mii,

1.000.000 este unitatea de cifre a cifrei de milioane etc.

Numărul din oricare dintre cifre arată numărul de unități din această cifră. Deci, numărul 9, pe locul sutelor de miliarde, înseamnă că numărul 38.001.102.987.000 128.425 include nouă miliarde (adică de 9 ori 1.000.000.000 sau unități de 9 biți ale miliardelor). O cifră goală de sute de chintilioane înseamnă că nu există sute de chintilioane în acest număr sau numărul lor este egal cu zero. În acest caz, numărul 38 001 102 987 000 128 425 se poate scrie astfel: 038 001 102 987 000 128 425.

Puteți scrie altfel: 000 038 001 102 987 000 128 425. Zerourile de la începutul numărului indică cifre goale de ordin înalt. De obicei, acestea nu sunt scrise, spre deosebire de zerourile din interiorul notației zecimale, care marchează în mod necesar cifrele goale. Deci, trei zerouri din clasa milioanelor înseamnă că cifrele sute de milioane, zeci de milioane și unități de milioane sunt goale.

1.5. Abrevieri în scrierea numerelor

La scrierea numerelor naturale se folosesc abrevieri. Aici sunt cateva exemple:

1.000 = 1 mie (o mie)

23.000.000 = 23 de milioane (douăzeci și trei de milioane)

5.000.000.000 = 5 miliarde (cinci miliarde)

203.000.000.000.000 = 203 trilioane (două sute trei trilioane)

107.000.000.000.000.000 = 107 sqd. (o sută șapte cvadrilioane)

1.000.000.000.000.000.000 = 1 kw. (un chintilion)

Blocul 1.1. Dicţionar

Alcătuiește un glosar de termeni și definiții noi din §1. Pentru a face acest lucru, în celulele goale, introduceți cuvintele din lista de termeni de mai jos. În tabel (la sfârșitul blocului), indicați pentru fiecare definiție numărul termenului din listă.

Blocul 1.2. Autoinstruire

În lumea numerelor mari

Economie .

1. Bugetul rusesc pt anul urmator va fi: 6328251684128 ruble.
2. Cheltuieli planificate pentru acest an: 5124983252134 ruble.
3. Veniturile țării au depășit cheltuielile cu 1203268431094 ruble.

Întrebări și sarcini

1. Citiți toate cele trei numere date
2. Scrieți cifrele din clasa milionului pentru fiecare dintre cele trei numere

1. Care secțiune din fiecare dintre numere aparține cifrei din poziția a șaptea de la sfârșitul notării numerelor?
2. Ce număr de unități de biți arată numărul 2 în primul număr?... în al doilea și al treilea număr?
3. Numiți unitatea de biți pentru poziția a opta de la sfârșit în notația a trei numere.

Geografie (lungime)

1. Raza ecuatorială a Pământului: 6378245 m
2. Circumferința ecuatorului: 40075696 m
3. Cea mai mare adâncime a oceanului mondial (Șanțul Marian din Oceanul Pacific) 11500 m

Întrebări și sarcini

1. Convertiți toate cele trei valori în centimetri și citiți numerele rezultate.
2. Pentru primul număr (în cm), scrieți numerele în secțiunile:

sute de mii _______

zeci de milioane _______

mii de _______

miliarde de _______

sute de milioane de _______

1. Pentru al doilea număr (în cm), notați unitățile de biți corespunzătoare numerelor 4, 7, 5, 9 din înregistrarea numărului

1. Convertiți a treia valoare în milimetri, citiți numărul rezultat.
2. Pentru toate pozițiile din înregistrarea celui de-al treilea număr (în mm), indicați cifrele și unitățile de cifre din tabel:

Geografie (pătrat)

1. Suprafața întregii suprafețe a Pământului este de 510.083 mii de kilometri pătrați.
2. Suprafața sumelor de pe Pământ este de 148.628 mii de kilometri pătrați.
3. Suprafața apei Pământului este de 361.455 mii de kilometri pătrați.

Întrebări și sarcini

1. Convertiți toate cele trei valori în metri patratiși citiți numerele rezultate.
2. Denumiți clasele și rangurile corespunzătoare cifrelor diferite de zero din înregistrarea acestor numere (în mp).
3. În introducerea celui de-al treilea număr (în mp), denumiți unitățile de biți corespunzătoare numerelor 1, 3, 4, 6.
4. În două intrări ale celei de-a doua valori (în km pătrați și în m²), indicați cărei cifre aparține numărul 2.
5. Notați unitățile de biți pentru numărul 2 în înregistrările celei de-a doua valori.

Blocul 1.3. Dialog cu un computer.

Se știe că numerele mari sunt adesea folosite în astronomie. Să dăm exemple. Distanța medie a Lunii de Pământ este de 384 mii km. Distanța Pământului de la Soare (medie) este de 149504 mii km, Pământul de Marte este de 55 milioane km. Pe un computer, folosind editorul de text Word, creați tabele astfel încât fiecare cifră din înregistrarea numerelor indicate să fie într-o celulă (celulă) separată. Pentru a face acest lucru, executați comenzile din bara de instrumente: tabel → adăugați tabel → număr de rânduri (puneți „1” cu cursorul) → număr de coloane (calculați-vă singur). Creați tabele pentru alte numere (bloc „Pregătire personală”).

Blocul 1.4. Stafeta de numere mari

Primul rând al tabelului conține un număr mare. Citește. Apoi finalizați sarcinile: mutând numerele din intrarea numerică la dreapta sau la stânga, obțineți următoarele numere și citiți-le. (Nu mutați zerourile de la sfârșitul numărului!). În clasă, ștafeta poate fi efectuată pasându-l unul altuia.

Randul 2 . Mutați toate cifrele numărului din prima linie spre stânga prin două celule. Înlocuiți numerele 5 cu numărul care îl urmează. Completați celulele goale cu zerouri. Citiți numărul.

Linia 3 . Mutați toate cifrele numărului din a doua linie spre dreapta prin trei celule. Înlocuiți numerele 3 și 4 din înregistrarea numărului cu următoarele numere. Completați celulele goale cu zerouri. Citiți numărul.

Linia 4. Mutați toate cifrele numărului din rândul 3 cu o celulă la stânga. Schimbați numărul 6 din clasa trilionului cu cel precedent, iar din clasa miliardului cu următorul număr. Completați celulele goale cu zerouri. Citiți numărul rezultat.

Linia 5 . Mutați toate cifrele numărului din rândul 4 cu o celulă la dreapta. Înlocuiți numărul 7 din locul „zeci de mii” cu cel precedent, iar din locul „zeci de milioane” cu următorul. Citiți numărul rezultat.

Linia 6 . Mutați toate cifrele numărului din rândul 5 la stânga după 3 celule. Schimbați numărul 8 din locul sute de miliarde cu cel anterior, iar numărul 6 din locul sute de milioane cu următorul număr. Completați celulele goale cu zerouri. Calculați numărul rezultat.

Linia 7 . Mutați toate cifrele numărului din rândul 6 la dreapta cu o celulă. Schimbați cifrele în zeci de cvadrilioane și zeci de miliarde de locuri. Citiți numărul rezultat.

Linia 8 . Mutați toate cifrele numărului din rândul 7 la stânga printr-o celulă. Schimbați cifrele în locurile de cinci miliarde și cvadrilioane. Completați celulele goale cu zerouri. Citiți numărul rezultat.

Linia 9 . Mutați toate cifrele numărului din rândul 8 la dreapta prin trei celule. Schimbați două numere adiacente în rândul de numere din clasele de milioane și trilioane. Citiți numărul rezultat.

Linia 10 . Mutați toate cifrele numărului din rândul 9 cu o celulă la dreapta. Citiți numărul rezultat. Evidențiați numerele care indică anul Olimpiadei de la Moscova.

Blocul 1.5. să ne jucăm

Aprinde un foc

Terenul de joc este un desen Brad de Crăciun. Are 24 de becuri. Dar doar 12 dintre ele sunt conectate la rețeaua electrică. Pentru a selecta lămpile conectate, trebuie să răspundeți corect la întrebări cu cuvintele „Da” sau „Nu”. Același joc poate fi jucat pe computer; răspunsul corect „aprinde” becul.

1. Este adevărat că numerele sunt semne speciale pentru scrierea numerelor naturale? (1 - da, 2 - nu)
2. Este adevărat că 0 este cel mai mic număr natural? (3 - da, 4 - nu)
3. Este adevărat că în sistemul numeric pozițional aceeași cifră poate desemna numere diferite? (5 - da, 6 - nu)
4. Este adevărat că un anumit loc în notația zecimală a numerelor se numește loc? (7 - da, 8 - nu)
5. Având în vedere numărul 543 384. Este adevărat că numărul celor mai semnificative cifre din acesta este 543, iar cel mai mic 384? (9 - da, 10 - nu)
6. Este adevărat că în clasa miliardelor, cea mai veche dintre unitățile de biți este de o sută de miliarde, iar cea mai tânără este de un miliard? (11 - da, 12 - nu)
7. Este dat numărul 458 121. Este adevărat că suma numărului cifrelor cele mai semnificative și a numărului celor mai puțin semnificative este 5? (13 - da, 14 - nu)
8. Este adevărat că cea mai veche dintre unitățile de un miliard de clasă este de un milion de ori mai mare decât cea mai veche dintre unitățile de un milion de clasă? (15 - da, 16 - nu)
9. Având în vedere două numere 637508 și 831. Este adevărat că cel mai semnificativ al primului număr este de 1000 de ori mai mare decât cel mai semnificativ al celui de-al doilea număr? (17 - da, 18 - nu)
10. Este dat numărul 432. Este adevărat că cea mai semnificativă unitate de biți a acestui număr este de 2 ori mai mare decât cea mai tânără? (19 - da, 20 - nu)
11. Având în vedere numărul 100 000 000. Este adevărat că numărul de unități de biți care formează 10 000 în el este 1000? (21 - da, 22 - nu)
12. Este adevărat că clasa trilionului este precedată de clasa cvadrilionului și că clasa quintilionului este precedată de acea clasă? (23 - da, 24 - nu)

1.6. Din istoria numerelor

Din cele mai vechi timpuri, omul s-a confruntat cu nevoia de a număra numărul de lucruri, de a compara numărul de obiecte (de exemplu, cinci mere, șapte săgeți ...; într-un trib sunt 20 de bărbați și treizeci de femei, .. .). Era, de asemenea, necesitatea stabilirii ordinii într-un anumit număr de obiecte. De exemplu, atunci când vânează, liderul tribului merge primul, cel mai puternic războinic al tribului vine pe al doilea și așa mai departe. În aceste scopuri s-au folosit numere. Pentru ei au fost inventate nume speciale. În vorbire, ele sunt numite numerale: unu, doi, trei etc. sunt numere cardinale, iar primul, al doilea, al treilea sunt numere ordinale. Numerele au fost scrise folosind caractere speciale - numere.

De-a lungul timpului au fost sisteme de numere. Acestea sunt sisteme care includ modalități de a scrie numere și diverse acțiuni asupra lor. Cele mai vechi sisteme de numere cunoscute sunt sistemele de numere egiptean, babilonian și roman. În Rusia, pe vremuri, literele alfabetului cu un semn special ~ (titlo) erau folosite pentru a scrie numere. Sistemul numeric zecimal este în prezent cel mai utilizat. Utilizate pe scară largă, în special în lumea computerelor, sunt sistemele de numere binare, octale și hexazecimale.

Deci, pentru a scrie același număr, puteți folosi diferite semne - numere. Deci, numărul patru sute douăzeci și cinci poate fi scris cu cifre egiptene - hieroglife:

Acesta este modul egiptean de a scrie numerele. Același număr în cifre romane: CDXXV(modul roman de a scrie numere) sau cifre zecimale 425 (notația zecimală a numerelor). În notație binară, arată astfel: 110101001 (notație binară sau binară a numerelor), iar în octal - 651 (notația octală a numerelor). În notație hexazecimală, se va scrie: 1A9(notație hexazecimală). Puteți face acest lucru simplu: faceți, ca Robinson Crusoe, patru sute douăzeci și cinci de crestături (sau lovituri) pe un stâlp de lemn - IIIIIIIII…... III. Acestea sunt primele imagini ale numerelor naturale.

Deci, în sistemul zecimal de scriere a numerelor (în modul zecimal de scriere a numerelor), sunt folosite cifre arabe. Acestea sunt zece caractere diferite - numere: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . În binar, două cifre binare: 0, 1; în octal - opt cifre octale: 0, 1, 2, 3, 4, 5, 6, 7; în hexazecimal - șaisprezece cifre hexazecimale diferite: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; în sexagesimal (babilonian) - șaizeci de caractere diferite - numere etc.)

Cifre zecimale au venit în țările europene din Orientul Mijlociu, țările arabe. De aici și numele - cifre arabe. Dar au venit la arabi din India, unde au fost inventați pe la mijlocul primului mileniu.

1.7. Sistemul numeric roman

Unul dintre sistemele de numere antice utilizate astăzi este sistemul roman. Prezintăm în tabel numerele principale ale sistemului numeric roman și numerele corespunzătoare ale sistemului zecimal.

numeral roman					C
				50 cincizeci		500 cinci sute	1000 de mii

Sistemul numeric roman este sistem de adăugare.În ea, spre deosebire de sistemele poziționale (de exemplu, zecimală), fiecare cifră denotă același număr. Da, înregistrează II- denotă numărul doi (1 + 1 = 2), notație III- numărul trei (1 + 1 + 1 = 3), notație XXX- numărul treizeci (10 + 10 + 10 = 30), etc. Următoarele reguli se aplică pentru scrierea numerelor.

1. Dacă numărul mai mic este după mai mare, apoi se adaugă la cea mai mare: VII- numărul șapte (5 + 2 = 5 + 1 + 1 = 7), XVII- numărul șaptesprezece (10 + 7 = 10 + 5 + 1 + 1 = 17), MCL- numărul o mie o sută cincizeci (1000 + 100 + 50 = 1150).
2. Dacă numărul mai mic este inainte de mai mare, atunci se scade din cea mai mare: IX- numărul nouă (9 = 10 - 1), LM- numărul nouă sute cincizeci (1000 - 50 = 950).

Pentru a scrie numere mari, trebuie să folosiți (inventați) caractere noi - numere. În același timp, intrările de numere se dovedesc a fi greoaie, este foarte dificil să se efectueze calcule cu cifre romane. Deci anul lansării primului satelit artificial de Pământ (1957) în notație romană are forma MCMLVII .

Blocul 1. 8. Card perforat

Citirea numerelor naturale

Aceste sarcini sunt verificate folosind o hartă cu cercuri. Să explicăm aplicația sa. După ce ați finalizat toate sarcinile și ați găsit răspunsurile corecte (sunt notate cu literele A, B, C etc.), puneți pe cartonaș o coală de hârtie transparentă. Marcați răspunsurile corecte cu semnele „X” pe el, precum și semnul combinat „+”. Apoi așezați foaia transparentă pe pagină, astfel încât semnele de aliniere să se potrivească. Dacă toate semnele „X” sunt în cercurile gri de pe această pagină, atunci sarcinile sunt finalizate corect.

1.9. Ordinea de citire a numerelor naturale

Când citiți un număr natural, procedați după cum urmează.

1. Împărțiți mental numărul în triple (clase) de la dreapta la stânga, de la sfârșitul introducerii numărului.

1. Începând de la clasa de juniori, de la dreapta la stânga (de la sfârșitul introducerii numărului), se notează numele claselor: unități, mii, milioane, miliarde, trilioane, cvadrilioane, chintilioane.
2. Citiți numărul, începând cu liceul. În acest caz, sunt apelate numărul de unități de biți și numele clasei.
3. Dacă cifra este zero (cifra este goală), atunci nu este apelată. Dacă toate cele trei cifre ale clasei apelate sunt zero (cifrele sunt goale), atunci această clasă nu este apelată.

Să citim (numim) numărul scris în tabel (vezi § 1), conform pașilor 1 - 4. Împărțim mental numărul 38001102987000128425 în clase de la dreapta la stânga: 038 001 102 987 000 128 425. Să indicăm numele. clasele din acest numar, incepand de la sfarsit intrarile sale sunt: ​​unitati, mii, milioane, miliarde, trilioane, cvadrilioane, chintilioane. Acum puteți citi numărul, începând cu clasa de seniori. Numim numere de trei cifre, două cifre și o cifră, adăugând numele clasei corespunzătoare. Clasele goale nu sunt denumite. Primim următorul număr:

• 038 - treizeci și opt de chintilioane
• 001 - un cvadrilion
• 102 - o sută două trilioane
• 987 - nouă sute optzeci și șapte de miliarde
• 000 - nu da nume (nu citeste)
• 128 - o sută douăzeci și opt de mii
• 425 - patru sute douăzeci și cinci

Ca urmare, numărul natural 38 001 102 987 000 128 425 se citește după cum urmează: „treizeci și opt de chintilioane un cvadrilion o sută două trilioane nouă sute optzeci și șapte de miliarde o sută douăzeci și opt de mii patru sute douăzeci și cinci”.

1.9. Ordinea scrierii numerelor naturale

Numerele naturale sunt scrise în următoarea ordine.

1. Notați trei cifre pentru fiecare clasă, începând cu clasa cea mai mare până la cifra unităților. În acest caz, pentru clasa superioară de numere, pot fi două sau unul.
2. Dacă clasa sau rangul nu este denumit, atunci zerouri sunt scrise în cifrele corespunzătoare.

De exemplu, numărul douăzeci și cinci de milioane trei sute două scris sub forma: 25 000 302 (clasa mii nu este numită, prin urmare, zerouri sunt scrise în toate cifrele clasei mii).

1.10. Reprezentarea numerelor naturale ca sumă de termeni de biți

Să dăm un exemplu: 7 563 429 este reprezentarea zecimală a numărului șapte milioane cinci sute șaizeci și trei de mii patru sute douăzeci și nouă. Acest număr conține șapte milioane, cinci sute de mii, șase zeci de mii, trei mii, patru sute, două zeci și nouă unități. Poate fi reprezentat ca o sumă: 7.563.429 \u003d 7.000.000 + 500.000 + 60.000 + + 3.000 + 400 + 20 + 9. O astfel de intrare se numește reprezentarea unui număr natural ca sumă de termeni de biți.

Blocul 1.11. să ne jucăm

Temnita Treasures

Pe terenul de joc este un desen pentru basmul lui Kipling „Mowgli”. Pe cinci cufere lacăte. Pentru a le deschide, trebuie să rezolvați problemele. În același timp, când deschizi un cufăr de lemn, primești un punct. Când deschizi un cufăr de tablă, primești două puncte, unul de cupru - trei puncte, unul de argint - patru și unul de aur unul - cinci. Câștigătorul este cel care deschide mai repede toate cuferele. Același joc poate fi jucat pe computer.

1. cufăr de lemn

Aflați câți bani (în mii de ruble) sunt în acest cufăr. Pentru a face acest lucru, trebuie să găsiți numărul total al unităților de biți cele mai puțin semnificative din clasa milioane pentru numărul: 125308453231.

1. Cufă de tablă

Aflați câți bani (în mii de ruble) sunt în acest cufăr. Pentru a face acest lucru, în numărul 12530845323 găsiți numărul unităților de biți cel mai puțin semnificative ale clasei de unități și numărul unităților de biți cele mai puțin semnificative ale clasei milioane. Apoi găsiți suma acestor numere și atribuiți în dreapta numărul în locul zecilor de milioane.

1. Cufă de cupru

Pentru a găsi banii acestui cufăr (în mii de ruble), în numărul 751305432198203 găsiți numărul unităților cu cele mai mici cifre din clasa trilionului și numărul unităților cu cele mai mici cifre din clasa miliardului. Apoi găsiți suma acestor numere și în dreapta atribuiți numerele naturale ale clasei de unități ale acestui număr în ordinea aranjamentului lor.

1. Cufăr de argint

Banii acestui cufăr (în milioane de ruble) vor fi afișați prin suma a două numere: numărul unităților cu cifrele cele mai mici din clasa miilor și unitățile cu cifre medii ale clasei de miliarde pentru numărul 481534185491502.

1. cufăr de aur

Având în vedere numărul 800123456789123456789. Dacă înmulțim numerele din cele mai mari cifre din toate clasele acestui număr, obținem banii acestui cufăr în milioane de ruble.

Blocul 1.12. Meci

Scrie numere naturale. Reprezentarea numerelor naturale ca sumă de termeni de biți

Pentru fiecare sarcină din coloana din stânga, alegeți o soluție din coloana din dreapta. Notează răspunsul sub forma: 1a; 2g; 3b…

	Notează numerele: cinci milioane douăzeci și cinci de mii
	Notează numerele: cinci miliarde douăzeci și cinci de milioane
	Notează numerele: cinci trilioane douăzeci și cinci
	Notează numerele:șaptezeci și șapte de milioane șaptezeci și șapte de mii șapte sute șapte și șapte
	Notează numerele:șaptezeci și șapte de trilioane șapte sute șapte și șapte de mii șapte
	Notează numerele:șaptezeci și șapte de milioane șapte sute șapte și șapte de mii șapte
	Notează numerele: o sută douăzeci și trei de miliarde patru sute cincizeci și șase de milioane șapte sute optzeci și nouă de mii
	Notează numerele: o sută douăzeci și trei de milioane patru sute cincizeci și șase de mii șapte sute optzeci și nouă
	Notează numerele: trei miliarde unsprezece
	Notează numerele: trei miliarde unsprezece milioane

Opțiunea 2

	treizeci și două de miliarde o sută șaptezeci și cinci de milioane două sute nouăzeci și opt de mii trei sute patruzeci și unu		100000000 + 1000000 + 10000 + 100 + 1
	Exprimați numărul ca sumă de termeni de biți: trei sute douăzeci și unu de milioane patruzeci și unu		30000000000 + 2000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Exprimați numărul ca sumă de termeni de biți: 321000175298341
	Exprimați numărul ca sumă de termeni de biți: 101010101
	Exprimați numărul ca sumă de termeni de biți: 11111		300000000 + 20000000 + 1000000 +
	5000000 + 300000 + 20000 + 1000
	Scrieți cu notație zecimală numărul reprezentat ca sumă a termenilor de biți: 5000000 + 300 + 20 + 1		30000000000000 + 2000000000000 + 1000000000000 + 100000000 + 70000000 + 5000000 + 200000 + 90000 + 8000 + 300 + 40 + 1
	Scrieți cu notație zecimală numărul reprezentat ca sumă a termenilor de biți: 10000000000 + 2000000000 + 100000 + 10 + 9
	Scrieți cu notație zecimală numărul reprezentat ca sumă a termenilor de biți: 10000000000 + 2000000000 + 100000000 + 10000000 + 9000000
	Scrieți cu notație zecimală numărul reprezentat ca sumă a termenilor de biți: 9000000000000 + 9000000000 + 9000000 + 9000 + 9		10000 + 1000 + 100 + 10 + 1

Blocul 1.13. Testul fațetelor

Numele testului provine de la cuvântul „ochi compus al insectelor”. Acesta este un ochi compus, format din „ochi” separati. Sarcinile testului fațetat sunt formate din elemente separate, indicate prin numere. De obicei, testele fațetate conțin un număr mare de sarcini. Dar există doar patru sarcini în acest test, dar sunt alcătuite dintr-un număr mare de elemente. Acest lucru se face pentru a vă învăța cum să „colectați” problemele de testare. Dacă le poți compune, atunci poți face față cu ușurință altor teste fațete.

Să explicăm cum sunt compuse sarcinile folosind exemplul celei de-a treia sarcini. Este alcătuit din elemente de testare numerotate: 1, 4, 7, 11, 1, 5, 7, 9, 10, 16, 17, 22, 21, 25

« În cazul în care un» 1) luați numere din tabel (număr); 4) 7; 7) plasați-l într-o categorie; 11) miliard; 1) ia un număr de la masă; 5) 8; 7) plasează-l în rânduri; 9) zeci de milioane; 10) sute de milioane; 16) sute de mii; 17) zeci de mii; 22) plasați numerele 9 și 6 în locurile cu mii și sute. 21) completați cifrele rămase cu zerouri; " APOI» 26) obținem un număr egal cu timpul (perioada) revoluției planetei Pluto în jurul Soarelui în secunde (s); " Acest număr este»: 7880889600 s. În răspunsuri, este indicat prin scrisoare "în".

Când rezolvați probleme, scrieți numerele din celulele tabelului cu un creion.

Testul fațetelor. Alcătuiește un număr

Tabelul conține numerele:

În cazul în care un

1) luați numărul (numerele) din tabel:

2) 4; 3) 5; 4) 7; 5) 8; 6) 9;

7) plasați această cifră (numerele) în categoria (cifre);

8) sute de cvadrilioane și zeci de cvadrilioane;

9) zeci de milioane;

10) sute de milioane;

11) miliarde;

12) chintilioane;

13) zeci de chintilioane;

14) sute de chintilioane;

15) trilioane;

16) sute de mii;

17) zeci de mii;

18) umple clasa (clasele) cu ea (ei);

19) chintilioane;

20) miliarde;

21) completați cifrele rămase cu zerouri;

22) așezați numerele 9 și 6 în locurile miilor și sutelor;

23) obținem un număr egal cu masa Pământului în zeci de tone;

24) obținem un număr aproximativ egal cu volumul Pământului în metri cubi;

25) obținem un număr egal cu distanța (în metri) de la Soare la cea mai îndepărtată planetă sistem solar Pluton;

26) obținem un număr egal cu timpul (perioada) revoluției planetei Pluto în jurul Soarelui în secunde (s);

Acest număr este:

a) 5929000000000

b) 999990000000000000000

d) 598000000000000000000

Rezolva probleme:

1, 3, 6, 5, 18, 19, 21, 23

1, 6, 7, 14, 13, 12, 8, 21, 24

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25

Răspunsuri

1, 3, 6, 5, 18, 19, 21, 23 - g

1, 6, 7, 14, 13, 12, 8, 21, 24 - b

1, 4, 7, 11, 1, 5, 7, 10, 9, 16, 17, 22, 21, 26 - în

1, 3, 7, 15, 1, 6, 2, 6, 18, 20, 21, 25 - a

Numerele naturale și proprietățile lor

Numerele naturale sunt folosite pentru a număra obiectele din viață. Orice număr natural folosește cifrele $0,1,2,3,4,5,6,7,8,9$

O succesiune de numere naturale, fiecare număr următor în care este $1$ mai mare decât cel precedent, formează o serie naturală care începe cu unu (pentru că unul este cel mai mic număr natural) și nu are cea mai mare valoare, adică fără sfârşit.

Zero nu este considerat un număr natural.

Urmărind proprietățile relației

Toate proprietățile numerelor naturale și operațiile asupra lor decurg din cele patru proprietăți ale relațiilor de succesiune, care au fost formulate în $1891$ de D. Peano:

Unul este un număr natural care nu urmează niciunui număr natural.

Fiecare număr natural este urmat de un singur număr

Fiecare număr natural, altul decât $1$, urmează unul și numai un număr natural

Submulțimea numerelor naturale care conține numărul $1$ și împreună cu fiecare număr numărul care îl urmează, conține toate numerele naturale.

Dacă înregistrarea unui număr natural este formată dintr-o cifră, se numește o singură cifră (de exemplu, $2,6,9$ etc.), dacă înregistrarea este formată din două cifre, se numește două cifre (de exemplu, $12,18 $ .45$), etc. În mod similar. Două cifre, trei cifre, patru cifre etc. numerele sunt numite multivalorice în matematică.

Proprietatea de adunare a numerelor naturale

Proprietate comutativă: $a+b=b+a$

Suma nu se modifică atunci când termenii sunt rearanjați

Proprietate asociativă: $a+ (b+c) =(a+b) +c$

Pentru a adăuga suma a două numere la un număr, puteți adăuga mai întâi primul termen, iar apoi, la suma rezultată, al doilea termen

Adăugarea zero nu schimbă numărul, iar dacă adăugați orice număr la zero, obțineți numărul adăugat.

proprietăți de scădere

Proprietatea de a scădea suma din numărul $a-(b+c) =a-b-c$ dacă $b+c ≤ a$

Pentru a scădea suma dintr-un număr, puteți scădea mai întâi primul termen din acest număr, iar apoi din diferența rezultată, al doilea termen

Proprietatea de a scădea un număr din suma $(a+b) -c=a+(b-c)$ dacă $c ≤ b$

Pentru a scădea un număr din sumă, îl puteți scădea dintr-un termen și adăugați un alt termen la diferența rezultată

Dacă scadeți zero dintr-un număr, numărul nu se va schimba.

Dacă îl scădeți din numărul în sine, obțineți zero

Proprietăți de multiplicare

Deplasarea $a\cdot b=b\cdot a$

Produsul a două numere nu se schimbă atunci când factorii sunt rearanjați

Asociativ $a\cdot (b\cdot c)=(a\cdot b)\cdot c$

Pentru a înmulți un număr cu produsul a două numere, îl puteți înmulți mai întâi cu primul factor și apoi să înmulțiți produsul rezultat cu al doilea factor.

Când este înmulțit cu unu, produsul nu se modifică $m\cdot 1=m$

Când este înmulțit cu zero, produsul este zero

Când nu există paranteze în notația produsului, înmulțirea se realizează în ordine de la stânga la dreapta

Proprietățile înmulțirii în raport cu adunarea și scăderea

Proprietatea distributivă a înmulțirii în raport cu adunarea

$(a+b)\cdot c=ac+bc$

Pentru a înmulți suma cu un număr, puteți înmulți fiecare termen cu acest număr și adăugați produsele rezultate

De exemplu, $5(x+y)=5x+5y$

Proprietatea distributivă a înmulțirii în raport cu scăderea

$(a-b)\cdot c=ac-bc$

Pentru a înmulți diferența cu un număr, înmulțiți minuendul și scădeți cu acest număr și scadeți al doilea din primul produs

De exemplu, $5(x-y)=5x-5y$

Comparația numerelor naturale

Pentru orice numere naturale $a$ și $b$, numai una dintre cele trei relații $a=b$, $a

Numărul mai mic este cel care apare mai devreme în seria naturală, iar cel mai mare care apare mai târziu. Zero este mai mic decât orice număr natural.

Exemplul 1

Comparați numerele $a$ și $555$, dacă se știe că există un număr $b$ și sunt valabile următoarele relații: $a

Soluţie: Pe baza proprietății specificate, deoarece prin conditia $a

orice submulțime de numere naturale care conține cel puțin un număr are cel mai mic număr

O submulțime în matematică este o parte a unei mulțimi. Se spune că o mulțime este o submulțime a alteia dacă fiecare element al submulțimii este și un element al mulțimii mai mari.

Adesea, pentru a compara numerele, își găsesc diferența și o compară cu zero. Dacă diferența este mai mare de $0$, dar primul număr mai mult de o secundă, dacă diferența este mai mică de $0$, atunci primul număr este mai mic decât al doilea.

Rotunjirea numerelor naturale

Când nu este necesară precizia completă sau nu este posibilă, numerele sunt rotunjite, adică sunt înlocuite cu numere apropiate cu zerouri la sfârșit.

Numerele naturale sunt rotunjite la zeci, sute, mii etc.

Când se rotunjește un număr la zeci, acesta este înlocuit cu cel mai apropiat număr format din zeci întregi; un astfel de număr are cifra $0$ în locul unităților

Când se rotunjește un număr la sute, acesta este înlocuit cu cel mai apropiat număr format din sute întregi; un astfel de număr ar trebui să aibă cifra $0$ în locul zecilor și unităților. etc

Numerele la care este rotunjit se numesc valoarea aproximativă a numărului cu o precizie a cifrelor specificate. De exemplu, dacă rotunjiți numărul $564$ la zeci, atunci obținem că poate fi rotunjit cu un dezavantaj și obținem 560$ sau cu un exces și primiți 570$.

Regula de rotunjire pentru numere naturale

Dacă în dreapta cifrei la care este rotunjit numărul este cifra $5$ sau o cifră mai mare de $5$, atunci la cifra acestei cifre se adaugă $1$; în caz contrar, această cifră rămâne neschimbată.

Toate cifrele situate în dreapta cifrei la care este rotunjit numărul sunt înlocuite cu zerouri

numere întregi- numerele naturale sunt numere care sunt folosite pentru a număra obiecte. Mulțimea tuturor numerelor naturale este uneori numită seria naturală: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 etc. .

Pentru a scrie numerele naturale se folosesc zece cifre: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Cu ajutorul lor, puteți scrie orice număr natural. Această notație se numește zecimală.

Seria naturală de numere poate fi continuată la nesfârșit. Nu există nici un număr care ar fi ultimul, pentru că unul poate fi întotdeauna adăugat la ultimul număr și se va obține un număr care este deja mai mare decât cel dorit. În acest caz, spunem că nu există cel mai mare număr în seria naturală.

Cifre ale numerelor naturale

În scrierea oricărui număr folosind numere, locul în care se află numărul în număr este crucial. De exemplu, numărul 3 înseamnă: 3 unități dacă este ultimul în număr; 3 zeci dacă va fi în numărul de pe penultimul loc; 4 sute, dacă ea va fi pe numărul de pe locul trei de la final.

Ultima cifră înseamnă cifra unităților, penultima - cifra zecilor, 3 de la sfârșit - cifra sutelor.

Cifre simple și multiple

Dacă există un 0 în orice cifră a numărului, aceasta înseamnă că nu există unități în această cifră.

Numărul 0 reprezintă zero. Zero este „niciunul”.

Zero nu este un număr natural. Deși unii matematicieni cred altfel.

Dacă un număr este format dintr-o cifră, se numește o singură cifră, două - două cifre, trei - trei cifre etc.

Numerele care nu sunt o singură cifră sunt numite și cifre multiple.

Clase de cifre pentru citirea numerelor naturale mari

Pentru a citi numere naturale mari, numărul este împărțit în grupuri de trei cifre, începând de la marginea dreaptă. Aceste grupuri se numesc clase.

Primele trei cifre de pe marginea dreaptă alcătuiesc clasa de unități, următoarele trei clasa de mii, următoarele trei clasa de milioane.

Un milion este o mie de mii, pentru înregistrare folosesc abrevierea milion 1 milion = 1.000.000.

Un miliard = o mie de milioane. Pentru înregistrare se folosește abrevierea billion 1 miliard = 1.000.000.000.

Exemplu de scriere și citire

Acest număr are 15 unități în clasa miliarde, 389 unități în clasa milioane, zero unități în clasa mii și 286 unități în clasa unități.

Acest număr arată astfel: 15 miliarde 389 milioane 286.

Citiți numerele de la stânga la dreapta. La rândul său, se numește numărul de unități ale fiecărei clase și apoi se adaugă numele clasei.